Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

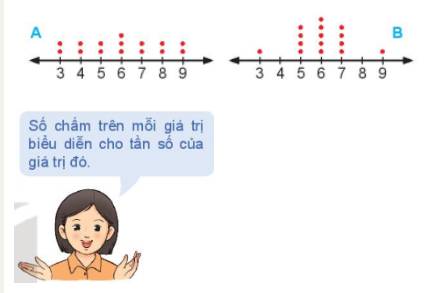
a) Cả 2 mẫu đều có n=15.
Ta có cả 2 mẫu đều có giá trị nhỏ nhất là 3, giá trị lớn nhất là 9
Do đó cả 2 mẫu cùng khoảng biến thiên.
Cả 2 biểu đồ này có dạng đối xứng nên giá trị trung bình của hai mẫu A và B bằng nhau.
b) Từ biểu đồ ta thấy, mẫu A có các số liệu đồng đều và ổn định hơn mẫu B nên phương sai của mẫu A nhỏ hơn mẫu B.

Khẳng định (1): Nếu các giá trị của mẫu số liệu càng tập trung quanh giá trị trung bình thì độ lệch của mỗi giá trị so với giá trị trung bình càng nhỏ (tức là \({x_i} - \overline x \) càng nhỏ, với \(i = 1;2;...;n\)), dẫn đến độ lệch chuẩn càng nhỏ.
\(\Rightarrow\)(1) Sai
Khẳng định (2): Khoảng biến thiên R bằng hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất nên chỉ sử dụng thông tin của giá trị lớn nhất và bé nhất
\(\Rightarrow\) (2) Đúng.
Khẳng định (3): Khoảng tứ phân vị \({\Delta _Q} = {Q_3} - {Q_1}\), các giá trị \({Q_1},{Q_3}\) không bị ảnh hưởng bởi giá trị của giá trị lớn nhất và giá trị nhỏ nhất (với n>4)
\(\Rightarrow\) Sai
Khẳng định (4): Khoảng tứ phân vị chính là khoảng biến thiên của 50% số liệu chính giữa của mẫu số liệu đã sắp xếp
\(\Rightarrow\) Sai.
Khẳng định (5): Các số đo độ phân tán là
Khoảng biến thiên R=Số lớn nhất – Số nhỏ nhất > 0
Trước khi tính khoảng tứ phân vị thì mẫu số liệu được sắp xếp theo thứ tự không giảm
\(\Rightarrow\) \({Q_3} > {Q_1}\) => \({\Delta _Q} = {Q_3} - {Q_1} > 0\)
Phương sai \({s^2} = \frac{{{{\left( {{x_1} - \overline x} \right)}^2} + {{\left( {{x_2} - \overline x} \right)}^2} + ... + {{\left( {{x_n} - \overline x} \right)}^2}}}{n} > 0\)
Độ lệch chuẩn: \(s = \sqrt {{s^2}} > 0\)
\(\Rightarrow\) Các số đo độ phân tán đều không âm
\(\Rightarrow\) (5) Đúng.

Có 50% giá trị của mẫu số liệu nằm giữa \({Q_1}\) và \({Q_3}\)
=> chọn B.

Ví dụ, ta có bảng đo chiều cao của các bạn trong tổ như sau:
160 | 162 | 164 | 165 | 172 | 174 | 177 | 178 | 180 |
a) Sắp xếp mẫu số liệu theo thứ tự không giảm ta được:
160 162 164 165 172 174 177 178 180
Số trung bình cộng của mẫu số liệu trên là:
\(\overline x = \frac{{160\;\; + 162\;\; + 164\;\;\; + \;\;165\;\; + \;172\;\; + \;174\;\; + \;177\; + \;\;178\; + \;180}}{9} = \frac{{1532}}{9}\)
Trung vị của mẫu số liệu trên là: Do mẫu số liệu trên có 9 số liệu ( lẻ ) nên trung vị \({Q_2} = 172\)
Tứ phân vị của mẫu số liệu trên là:
- Trung vị của dãy 160 162 164 165 là: \({Q_1} = 163\)
- Trung vị của dãy 174 177 178 180 là: \({Q_3} = 177,5\)
- Vậy tứ phân vị của mẫu số liệu là: \({Q_1} = 163\), \({Q_2} = 172\), \({Q_3} = 177,5\)
b) Khoảng biến thiên của mẫu số liệu trên là: \(R = {x_{\max }} - {x_{\min }} = 180 - 160 = 20\)
Khoảng tứ phân vị của mẫu số liệu trên là: \({\Delta _Q} = {Q_3} - {Q_1} = 177,5 - 163 = 14,5\)
c) Phương sai của mẫu số liệu trên là:
\({s^2} = \frac{{\left[ {{{\left( {160 - \overline x } \right)}^2} + {{\left( {162 - \overline x } \right)}^2} + ... + {{\left( {180 - \overline x } \right)}^2}} \right]}}{9} \approx 50,84\)
Độ lệch chuẩn của mẫu số liệu trên là: \(s = \sqrt {{s^2}} \approx 7,13\)

Mẫu 1:
+) Số trung bình: \(\overline x = \frac{{0,1 + 0,3 + 0,5 + 0,5 + 0,3 + 0,7}}{6} = 0,4\)
+) Phương sai \({S^2} = \frac{1}{6}\left( {0,{1^2} + 0,{3^2} + 0,{5^2} + 0,{5^2} + 0,{3^2} + 0,{7^2}} \right) - 0,{4^2} \approx 0,0367\)
+) Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 0,19\)
Mẫu 2:
+) Số trung bình: \(\overline x = \frac{{1,1 + 1,3 + 1,5 + 1,5 + 1,3 + 1,7}}{6} = 1,4\)
+) Phương sai \({S^2} = \frac{1}{6}\left( {1,{1^2} + 1,{3^2} + 1,{5^2} + 1,{5^2} + 1,{3^2} + 1,{7^2}} \right) - 1,{4^2} \approx 0,0367\)
+) Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 0,19\)
Mẫu 3:
+) Số trung bình: \(\overline x = \frac{{1 + 3 + 5 + 5 + 3 + 7}}{6} = 4\)
+) Phương sai \({S^2} = \frac{1}{6}\left( {{1^2} + {3^2} + {5^2} + {5^2} + {3^2} + {7^2}} \right) - {4^2} \approx 3,67\)
+) Độ lệch chuẩn \(S = \sqrt {{S^2}} \approx 1,9\)
Kết luận:
Số liệu ở mẫu 2 hơn số liệu ở mẫu 1 là 1 đơn vị, số trung bình của mẫu 2 hơn số trung bình mẫu 1 là 1 đơn vị, còn phương sai và độ lệch chuẩn là như nhau.
Số liệu ở mẫu 3 gấp 10 lần số liệu mẫu 1, số trung bình, phương sai và độ lệch chuẩn của mẫu 3 lần lượt gấp 10 lần, 100 lần và 10 lần mẫu 1.

Các khẳng định đúng là: (1) ; (2); (3)
(4) cần sửa thành: Phương sai là bình phương của độ lệch chuẩn.
Chọn C

Câu 3:
Theo đề, ta có;
\(\left\{{}\begin{matrix}4a+2b+c=3\\-\dfrac{b}{2a}=1\\-\dfrac{b^2-4ac}{4a}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\b^2-4ac=-8a\\4a+2b+c=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\4a^2-4ac=-8a\\4a+2b+c=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\4a\left(a-c\right)=4a\cdot\left(-2\right)\\4a+2b+c=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\c=a+2\\4a-4a+a+2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-2\\c=3\end{matrix}\right.\)
Câu 3:
Theo đề, ta có;
\(\left\{{}\begin{matrix}4a+2b+c=3\\-\dfrac{b}{2a}=1\\-\dfrac{b^2-4ac}{4a}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\b^2-4ac=-8a\\4a+2b+c=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\4a^2-4ac=-8a\\4a+2b+c=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\4a\left(a-c\right)=4a\cdot\left(-2\right)\\4a+2b+c=3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\c=a+2\\4a-4a+a+2=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\b=-2\\c=3\end{matrix}\right.\)
Độ lệch chuẩn bằng căn bậc hai của phương sai.
=> Mẫu nào có phương sai lớn hơn thì có độ lệch chuẩn lớn hơn.
Chọn A.