Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A
@ Lời giải:
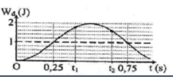
Với mốc thế năng được chọn tại vị trí cân bằng của lò xo, trục Ox hướng lên → E h d = m g x → đường nét đứt ứng với đồ thị thế năng hấp dẫn.
E d h = 0 , 5 k ( Δ l 0 – x ) 2 → ứng với đường nét liền.
+ Từ đồ thị, ta có: x m a x = A = 5 c m ; E d h m a x = m g A ↔ 0 , 05 = m . 10 . 0 , 05 → m = 0,1 kg.
E d h m a x = 0 , 5 k ( Δ l + A ) 2 ↔ 0 , 1125 = 0 , 5 . k ( 0 , 025 + 0 , 05 ) 2 → k = 40 N/m.
+ Khi vật đi qua vị trí lò xo không biến dạng → x = Δ l 0 = 0 , 5 A = 2 , 5 c m .
→ v = 3 2 v m a x = 3 2 40 0 , 1 .5 = 86 , 6 cm/s.

Đáp án A
Từ hình vẽ : A = 5 cm
Vị trí lò xo không biến dạng có Δℓ = 0 → Etdh = 0 → x = 2,5 cm (trên hình)
Thang chia trên trục tung: 9 khoảng = 0,1125 J → 4 khoảng = 0,05J = Et hd max
Ta có: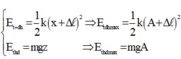


Áp dụng biểu thức độc lập, tốc độ của vật khi qua vị trí lò xo không biến dạng:
![]()

Chọn đáp án A
@ Lời giải:
Với mốc thế năng được chọn tại vị trí cân bằng của lò xo, trục Ox hướng lên → Ehd = mgx → đường nét đứt ứng với đồ thị thế năng hấp dẫn.
Edh = 0,5k(Δl0 – x)2 → ứng với đường nét liền.
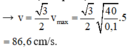
+ Từ đồ thị, ta có: xmax = A = 5 cm; Edhmax = mgA ↔ 0,05 = m.10.0,05 → m = 0,1 kg.
Edhmax = 0,5k(Δl + A)2 ↔ 0,1125 = 0,5.k(0,025 + 0,05)2 → k = 40 N/m.
+ Khi vật đi qua vị trí lò xo không biến dạng → x = Δl0 = 0,5A = 2,5 cm.
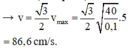

Do gia tốc: \(a=-\omega^2 x\) , nên gia tốc là hàm bậc nhất với li độ, và \(-A \leq x \leq A\) nên đồ thị gia tốc, li độ có dạng đoạn thẳng.
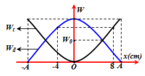

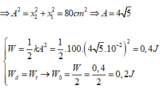
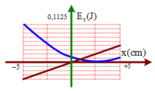
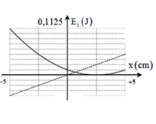
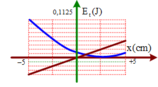
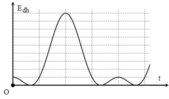

Động năng: \(W_đ=\frac{1}{2}k.x^2\)
Như vậy động năng tỉ lệ với li độ theo hàm bậc 2, do đó đồ thị biểu diễn sự phụ thuộc của động năng theo li độ là parabol.
Đáp án B.
đáp án là B