Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Ta có: ![]()
Gọi A là biến cố “trong 3 người được chọn đó không có 2 người ngồi kề nhau”
=> A ¯ là biến cố “trong 3 người đươc chọn có ít nhất 2 người ngồi kề nhau”
![]()

TH 1: 3 người ngồi kề nhau có 13 cách chọn.
TH 2: có 2 người ngồi cạnh nhau
- Hai người ngồi cạnh nhau ngồi đầu hàng có 2 cách chọn, với mỗi cách chọn như vậy có 12 cách chọn người còn lại vậy có: 2.12=24 cách.
- Hai người ngồi cạnh nhau không ngồi đầu hàng có 12 cách chọn, với mỗi cách chọn như vậy có 11 cách chọn người còn lại vậy có: 11.12=132 cách.
![]()
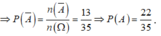

Số kết quả có thể là C520C205.
Số kết quả thuận lợi là số cách chọn 5 số trong tập [1,2,…,10][1,2,…,10]. Do đó, số kết quả thuận lợi là C510C105.
Vậy xác suất cần tìm là C510C520≈0,016
đúng ko

Đáp án B
Có n ( Ω ) = C 12 3
Giả sử chọn 3 người có số thứ tự trong hàng lần lượt là a, b, c
Theo giả thiết ta có: a < b < c, b – a > 1, c – b > 1, a , b , c ∈ { 1 , 2 , . . . , 12 } .

Bạn bị ngược rồi, B có 3 người còn A có 4 người mà. Không sao vẫn tính là bạn đang sắp xếp A nhé, mình kí hiệu 4 học sinh A là A1 A2 A3 A4 thì ở chỗ xếp học sinh A ấy bạn mới chỉ xếp cho A1, A2, A3 hoặc A4 mà thôi nên phải nhân 4 nữa. Đáp án phải là D
D.Công Thiện: Uh mình nhìn nhầm. Nhưng đáp án không thay đổi bạn ơi. Chỉ cần thay B bằng A thôi mà.

n(Ω)=8!
A là biến cố vợ chồng anh X ngồi gần nhau A=7*6!
=>p(a)=(7*6!)/8!=1/8
Đáp án C.