Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nối hai đường chéo của hình thoi lại=>Ta dc 4 tam giác bằng nhau trong hình thời đó.
Áp dụng định lí Pytago vào từng tam giác đó,ta tính đc:
Nửa mỗi đường chéo.
Từ đó ta tính dc các đg chéo của hình thoi.

Ta có:
\(a\cdot b=ab\left(a+b=12\right)\)
Mà:\(a\cdot b=\left(a-1\right)\left(b+1\right)\)
\(\Rightarrow\)Không có hình nào có diện tích lớn nhất

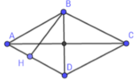
Xét hình thoi ABCD có hai đường chéo AC và BD vuông góc với nhau. Kẻ BH vuông góc với AD. Ta có SABCD = AD. BH
Trong tam giác vuông ABH vuông tại H thì:
BH ≤ AB (đường vuông góc ngắn hơn đường xiên)
Do đó: SABCD = AD. BH ≤ AD. AB = AB. AB = AB2
SABCDcó giá tị lớn nhất bằng AB2 khi ABCD là hình vuông.
Vây trong các hình thoi có cùng chu vi thì hình vuông có diện tích lớn nhất.
Đáp án cần chọn là: A

các hình thoi có cùng chu vi, hình vuông có diện tích lớn nhất.
tk nha bạn

Giả sử hình có hình thang ABCD mà AD = AB = BC = a
Từ B kẻ BE // AD => DE = BE = a
Gọi BH là đường cao của hình thang => HE = HC đặt HE = x. Vậy ta có \(BH=\sqrt{a^2-x^2}\)
Diện tích hình thang ABCD là:
\(S=\frac{AB+DC}{2}.BH=\frac{a+a+2x}{2}.\sqrt{a^2-x^2}\)
\(=\left(a+x\right)\sqrt{a^2-x^2}=\sqrt{\left(a+x\right)^2\left(a^2-x^2\right)}\)
\(=\sqrt{27\left(a-x\right).\frac{a+x}{3}.\frac{a+x}{3}.\frac{a+x}{3}}\)(1)
Muốn S lớn nhất thì vế phải của (1) lớn nhất. Mặt khác ta có:
\(\left(a-x\right)+\frac{a+x}{3}+\frac{a+x}{3}+\frac{a+x}{3}=2a\)không đổi, nên S lớn nhất khi \(a-x=\frac{a+x}{3}\Rightarrow a=2x\)
Như vậy hình thang có ba cạnh bằng nhau thì hình thang có một góc bằng 600 có diện tích lớn nhất.

1) hình tự vẽ nhé
a) Vì ABCD là hình thoi (gt)
\(\Rightarrow AB=BC\left(đn\right)\)
\(\Rightarrow\Delta ABC\)cân tại B
Mà \(\widehat{B}=60^0\)
\(\Rightarrow\Delta ABC\)là tam giác đều
b) Vì \(\Delta ABC\)đều(cmt)\(\Rightarrow AB=BC=AC=a\)
Gọi O là giao điểm 2 đường chéo BD và AC
Vì ABCD là hình thoi (gt) \(\Rightarrow DB\perp AC\left(tc\right)\)
\(\Rightarrow BO\perp AC\)
Vì tam giác ABC đều mà trong tam giác ABC thì BO là đường cao ứng với cạnh AC
\(\Rightarrow BO\)là đường trung tuyến ứng vs cạnh AC(tc)
\(\Rightarrow O\)là trung điểm của AC
\(\Rightarrow AO=OC=\frac{1}{2}AC=\frac{1}{2}a\)
Áp dụng định lý Py-ta-go vào tam giác BOC vuông tại O ta được:
\(BO^2+OC^2=BC^2\)
\(BO^2+\frac{1}{4}a^2=a^2\)
\(BO^2=\frac{3}{4}a^2\)
\(\Rightarrow BO=\frac{\sqrt{3}}{2}a\)
Ta có: \(S_{ABC}=\frac{1}{2}BO.AC=\frac{1}{2}.\frac{\sqrt{3}a}{2}.a\)
\(=\frac{\sqrt{3}}{4}a^2\)
CMTT \(S_{ADC}=\frac{\sqrt{3}}{4}a^2\)
\(S_{ABCD}=S_{ADC}+S_{ABC}=\frac{\sqrt{3}}{2}a^2\)

Bn ko có hình nên mik sẽ trả lời theo cảm tính,mong bn thông cảm nha:
Diện tích của các hình thoi nào có cạnh bằng a thì đều bằng nhau.Vì:
Hình thoi có bốn cạnh bằng nhau nên các hình thoi đó bằng nhau (theo tính chất hình thoi).
Vậy ko có hình thoi nào có diện tích lớn nhất vì các hình thoi đều bằng nhau.