Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số có đồ thị là một hình parabol, bề lõm quay xuống dưới.
Hình ảnh hình học có tính đối xứng.

Chọn D.
Theo công thức tính độ dài cung ta có độ dài cung có số đo 3,85 rad là
l = R.α = 8,43.3,85 = 32,4555 cm.

Áp dụng định lí cosin trong tam giác ABC ta có:
\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB.\cos A\)
\(\begin{array}{l} \Leftrightarrow B{C^2} = 7,{5^2} + 3,{5^2} - 2.7,5.3,5.\cos {135^o}\\ \Leftrightarrow B{C^2} \approx 105,6\\ \Leftrightarrow BC \approx 10,3\end{array}\)
Áp dụng định lí sin trong tam giác ABC ta có: \(\frac{{BC}}{{\sin A}} = 2R\)
\( \Rightarrow R = \frac{{BC}}{{2.\sin A}} = \frac{{10,3}}{{2.\sin {{135}^o}}} \approx 7,3\)

Gọi phương trình chuyển động của quả bóng có dạng \(y=at^2+bt+c\)
\(t=0;y=1\Rightarrow c=1\)
\(t=1;y=7\Rightarrow a+b+1=7\Rightarrow a+b=6\)
\(t=2;y=9\Rightarrow4a+2b+1=9\Rightarrow2a+b=4\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=6\\2a+b=4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-2\\b=8\end{matrix}\right.\)
\(\Rightarrow y=-2t^2+8t+1\)
Các thời điểm mà độ cao quả bóng đạt 7m là:
\(-2t^2+8t+1=7\Rightarrow2t^2-8t+6=0\)
\(\Rightarrow\left[{}\begin{matrix}t=1\\t=3\end{matrix}\right.\)
Vậy quả bóng đạt độ cao lớn hơn 7m trong khoảng thời gian 2s (từ giây thứ 1 đến giây thứ 3)
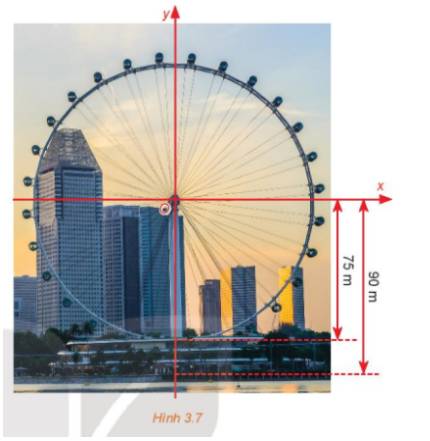
Một quả bóng chuyền được phát lên từ độ cao 1 m và chuyển động theo quỹ đạo là một cung parabol. Quả bóng đạt độ cao 7 m sau 1 giây và đạt độ cao 9 m sau 2 giây. Trong khoảng thời gian bao lâu thì độ cao quả bóng nhỏ hơn 7 m.

Tham khảo:
Giả sử chiếc đu quay quay theo chiều kim đồng hồ.
Gọi M là vị trí của cabin, M’ là vị trí của cabin sau 20 phút và các điểm A A’, B, H như hình dưới.
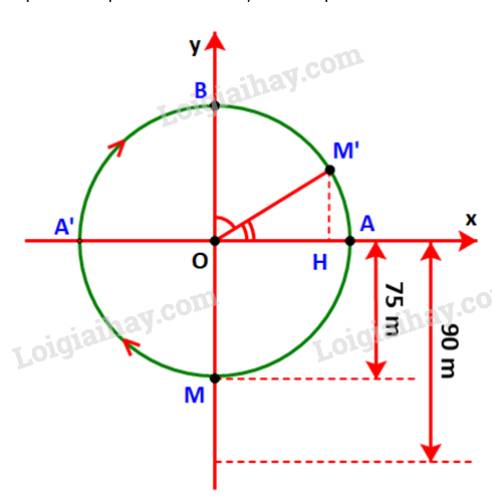
Vì đi cả vòng quay mất 30 phút nên sau 20 phút, cabin sẽ đi quãng đường bằng \(\frac{2}{3}\) chu vi đường tròn.
Sau 15 phút cabin đi chuyển từ điểm M đến điểm B, đi được \(\frac{1}{2}\) chu vi đường tròn.
Trong 5 phút tiếp theo cabin đi chuyển từ điểm B đến điểm M’ tương ứng \(\frac{1}{6}\) chu vi đường tròn hay \(\frac{1}{3}\) cung .
Do đó: \(\widehat {BOM'} = \frac{1}{3}{.180^o} = {60^o}\)\( \Rightarrow \widehat {AOM'} = {90^o} - {60^o} = {30^o}.\)
\( \Rightarrow M'H = \sin {30^o}.OM' = \frac{1}{2}.75 = 37,5\left( m \right).\)
\( \Rightarrow \) Độ cao của người đó là: 37,5 + 90 = 127,5 (m).
Vậy sau 20 phút quay người đó ở độ cao 127,5 m.


- Cách 1:
Hàm số biểu diễn đồ thị \(y = - 0,00188{\left( {x - 251,5} \right)^2} + 118\)
\(\begin{array}{l}{\left( {x - 251,5} \right)^2} \ge 0\\ \Leftrightarrow - 0,00188{\left( {x - 251,5} \right)^2} \le 0\\ \Leftrightarrow - 0,00188{\left( {x - 251,5} \right)^2} + 118 \le 118\end{array}\)
Khi đó độ cao y (m) của một điểm thuộc vòng cung thành cầu cảng Sydney đạt giá trị lớn nhất là \(y = 118\left( m \right)\)
- Cách 2:
Ta có phương trình thành cầu: \(y = – 0,00188(x – 251,5)^2 + 118\)
\( \Leftrightarrow y = – 0,00188x^2 + 0,94564x – 0,91423\), là hàm số bậc hai.
Vì a = – 0,00188 < 0 nên đồ thị hàm số trên có bề lõm hướng xuống dưới hay đỉnh I của đồ thị là điểm cao nhất, vậy giá trị lớn nhất cần tìm chính là tung độ của đỉnh I.
Ta có: \(b = 0,94564, c = – 0,91423\)
\( x_I = \frac{-b}{2a}= \frac{-0,94564}{2. (-0,00188)}=251,5 \Rightarrow y_I = – 0,00188(x_I – 251,5)^2 + 118 =118.\)
Vậy độ cao lớn nhất cần tìm là 118 m.