trị tuyệt đối(3 *x-5)+trị tuyệt đối(3 *x+1) = 6

K

Khách

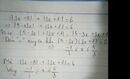
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

TN

trần nguyễn việt anh

26 tháng 12 2020 - olm

trị tuyệt đối(3 *x-5)+trị tuyệt đối(3 *x+1) = 6

1

LS

lysami -sama

26 tháng 12 2020

Chữ hơi xấu thông cảm:))

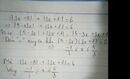
Bài tập Tất cả

Bài tập Tất cả

Các câu hỏi dưới đây có thể giống với câu hỏi trên

LD

Lê Đình Đạt

23 tháng 8 2021 - olm

TÌM GTNN CỦA A= TRỊ TUYỆT ĐỐI CỦA X-1 + TRỊ TUYỆT ĐỐI CỦA X-2 + TRỊ TUYỆT ĐỐI CỦA X-3 + TRỊ TUYỆT ĐỐI CỦA X-4 + TRỊ TUYỆT ĐỐI CỦA X-5 + TRỊ TUYỆT ĐỐI CỦA X-6 + TRỊ TUYỆT ĐỐI CỦA X-7 + TRỊ TUYỆT ĐỐI CỦA X-8

0

S

Seohyun

21 tháng 9 2016 - olm

A= 2x mũ 2 - 5x + 1 biết giá trị tuyệt đối của x = 1/3Các bạn nhớ giải rõ cho mình nha !Bài 2a,giá trị tuyệt đối của x =4,5b,giá trị tuyệt đối của x+1=6c, giá trị tuyệt đối của (1/4 +x ) -3,1 = 1,1d, giá trị tuyệt đối của x=0e,giá trị tuyệt đối của x=-1 và 2/5f,2. giá trị tuyệt đối của (x-3) -5 =3g, giá trị tuyệt đối của 0,5 -x = giá trị tuyệt đối của...

0

LD

Lê Đình Đạt

22 tháng 8 2021 - olm

Câu 15. Tìm GTNN của: a) A= trị tuyệt đối của x-1 + trị tuyệt đối của x+1 + trị tuyệt đối của x-2 + trị tuyệt đối của x-3

b) B= trị tuyệt đối của x+1 + trị tuyệt đối của x-1 + trị tuyệt đối của 2x-5

0

LD

Lê Đình Đạt

23 tháng 8 2021 - olm

TÌM GTNN CỦA :

a) A= TRỊ TUYỆT ĐỐI CỦA X-1 + TRỊ TUYỆT ĐỐI CỦA X+1 + TRỊ TUYỆT ĐỐI CỦA X-2 + TRỊ TUYỆT ĐỐI CỦA X-3

b) B= TRỊ TUYỆT ĐỐI CỦA X+1 + TRỊ TUYỆT ĐỐI CỦA X-1 + TRỊ TUYỆT ĐỐI CỦA 2X-5

1

NH

Nguyễn Huy Tú

23 tháng 8 2021

a, \(A=\left|x-1\right|+\left|x+1\right|+\left|x-2\right|+\left|x-3\right|\ge\left|1-x+x+1\right|+\left|2-x+x-3\right|=3\)

Dấu ''='' xảy ra khi \(\left(1-x\right)\left(x+1\right)\ge0;\left(2-x\right)\left(x-3\right)\ge0\Leftrightarrow-1\le x\le1;2\le x\le3\Leftrightarrow-1\le x\le3\)

Vậy GTNN của A bằng 3 tại -1 =< x =< 3

b, \(B=\left|x+1\right|+\left|x-1\right|+\left|2x-5\right|\ge\left|x+1+x-1\right|+\left|2x-5\right|\)

\(=\left|2x\right|+\left|2x-5\right|=\left|2x\right|+\left|5-2x\right|\ge\left|2x+5-2x\right|=5\)

Dấu ''='' xảy ra khi \(\left(x+1\right)\left(x-1\right)\ge0;2x\left(5-2x\right)\ge0\Leftrightarrow;0\le x\le\frac{5}{2}\)

Vậy GTNN của B bằng 5 tại 0 =< x =< 5/2

TA

TNViet anh

27 tháng 12 2020 - olm

trị tuyệt đối(5 *x+1)+trị tuyệt đối(3 -2 *x) = trị tuyệt đối(4 +3 *x)

1

XO

Xyz OLM

27 tháng 12 2020

Ta có : |5x + 1| + |3 - 2x| \(\ge\left|5x+1+3-2x\right|=\left|4+3x\right|\)

Dấu "=" xảy ra <=> \(\left(5x+1\right)\left(3-2x\right)\ge0\)

Xét các trường hợp

TH1 : \(\hept{\begin{cases}5x+1\ge0\\3-2x\ge0\end{cases}}\Rightarrow\hept{\begin{cases}x\ge-0,2\\x\le1,5\end{cases}}\Rightarrow-0,2\le x\le1,5\)

TH2 :\(\hept{\begin{cases}5x+1\le0\\3-2x\le0\end{cases}}\Rightarrow\hept{\begin{cases}x\le-0,2\\x\ge1,5\end{cases}}\Rightarrow x\in\varnothing\)

Vậy \(-0,2\le x\le1,5\)là giá trị cần tìm

LN

Lê Nguyễn Trung Đan

10 tháng 10 2020 - olm

a)Giá trị tuyệt đối của x+3 cộng giá trị tuyệt đối x-2 trừ 4x bằng 0( Mình đang cần giải gấp)

b)Giá trị tuyệt đối của x+1/3 trừ giá trị tuyệt đối của x- 1/2 cộng 2x trừ 5/6 bằng 0

0

NN

nguyen ngoc tri

6 tháng 7 2017 - olm

tìm x biết

giá trị tuyệt đối x+2/3 =3/5

giá trị tuyệt đối x - 2,8 =1/5

giá trị tuyệt đối x + 1/2 +3 = 0

giá trị tuyệt đối 2x - 3/8 = 0

2

S

Sarah

6 tháng 7 2017

Ta có : \(\left|x+\frac{2}{3}\right|=\frac{3}{5}\)

\(\Leftrightarrow\orbr{\begin{cases}x+\frac{2}{3}=\frac{3}{5}\\x+\frac{2}{3}=-\frac{3}{5}\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=\frac{3}{5}-\frac{2}{3}\\x=-\frac{3}{5}-\frac{2}{3}\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=-\frac{1}{15}\\x=-\frac{19}{15}\end{cases}}\)

HD

Hoàng Diệu Nhi

6 tháng 7 2017

/x/+2/3=3/5 hoặc /x/+2/3=-3/5

x=3/5-2/3 x=-3/5-2/3

x=-1/15 x=-19/15

/x/-2,8=1/5 hoặc /x/-2,8=-1/5

x=1/5+2,8 x=-1/5+2,8

x=3 x=13/5

/x/+1/2+3=0

x+7/2=0

x=0-7/2

x=-7/2

/2x/-3/8=0

2x=0+3/8

2x=3/8

x=3/8:2

x=3/16

D

dghdgh

13 tháng 8 2018 - olm

Tìm x biết : giá trị tuyệt đối của 5 - x = 7 -x

giá trị tuyệt đối của x + giá trị tuyệt đối của x + 1 + ..... + giá trị tuyệt đối của x + 3 = 6x

giá trị tuyệt đối của x + 2 cộng với giá trị tuyệt đối của x + 3 = x

0

KT

kim taehyung

21 tháng 10 2023

trị tuyệt đối(x-3.2)+trị tuyệt đối((2*x-1) /5) = x+3

2

NL

Nguyễn Lê Phước Thịnh

21 tháng 10 2023

loading...

NT

nguyễn thị hương giang

21 tháng 10 2023

\(\left|x-3,2\right|+\left|\dfrac{2x-1}{5}\right|=x+3\) (1)

TH1: \(\left\{{}\begin{matrix}x>3,2\Rightarrow\left|x-3,2\right|=x-3,2\\x>\dfrac{1}{2}\Rightarrow\left|\dfrac{2x-1}{5}\right|=\dfrac{2x-1}{5}\end{matrix}\right.\)

\(\left(1\right)\Rightarrow x-3,2+\dfrac{2x-1}{5}=x+3\)

\(\Rightarrow5x-16+2x-1=5x+15\Rightarrow2x=32\Leftrightarrow x=16\left(tm\right)\)

TH2: \(\left\{{}\begin{matrix}x>3,2\Rightarrow\left|x-3,2\right|=x-3,2\\x< \dfrac{1}{2}\Rightarrow\left|\dfrac{2x-1}{5}\right|=\dfrac{1-2x}{5}\end{matrix}\right.\)

\((1)\)\(\Rightarrow x-3,2+\dfrac{1-2x}{5}=x+3\Rightarrow5x-16+1-2x=5x+15\)

\(\Rightarrow-2x=0\Rightarrow x=0\left(l\right)\)

TH3: \(\left\{{}\begin{matrix}x< 3,2\Rightarrow\left|x-3,2\right|=3,2-x\\x>\dfrac{1}{2}\Rightarrow\left|\dfrac{2x-1}{5}\right|=\dfrac{2x-1}{5}\end{matrix}\right.\)

\(\left(1\right)\Rightarrow3,2-x+\dfrac{2x-1}{5}=x+3\)

\(\Rightarrow16-5x+2x-1=5x+15\Rightarrow8x=0\Leftrightarrow x=0\left(l\right)\)

TH4: \(\left\{{}\begin{matrix}x< 3,2\Rightarrow\left|x-3,2\right|=3,2-x\\x< \dfrac{1}{2}\Rightarrow\left|\dfrac{2x-1}{5}\right|=\dfrac{1-2x}{5}\end{matrix}\right.\)

\(\left(1\right)\Leftrightarrow3,2-x+\dfrac{1-2x}{5}=x+3\)

\(\Rightarrow16-5x+1-2x=5x+15\Rightarrow12x=2\Rightarrow c=\dfrac{1}{6}\left(tm\right)\)

Vậy \(x=\left\{16;\dfrac{1}{6}\right\}\)

LT

lê trà my

21 tháng 8 2019

tìm giá trị nhỏ nhất của B=trị tyệt đối (x-1)+trị tuyệt đối(x-3)+trị tuyệt đối(x-5)+trị tuyệt đối (x-7)+trị tuyệt đối (x-9)

mình cần gấp trong tối nay. Giúp mk nhanh nha.

0