Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

nh 98): Xét ΔABC và ΔABD có:
Nên ΔABC = ΔABD (g.c.g)
- Hình 99): Ta có:
Xét ΔABD và ΔACE có:
Nên ΔABD = ΔACE ( g.c.g)
Xét ΔADC và ΔAEB có:
DC = EB (Vì DC = DB + BC ; EB = EC + BC mà DB = EC)
Nên ΔADC = ΔAEB (g.c.g)
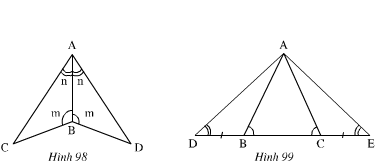
Xem hình 98)
∆ABC và ∆ABD có:
ˆA1A1^=ˆA2A2^(gt)
AB là cạnh chung.
ˆB1B1^=ˆB2B2^(gt)
Nên ∆ABC=∆ABD(g.c.g)
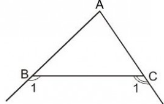
Xem hình 99)
Ta có:
ˆB1B1^+ˆB2B2^=1800 (Hai góc kề bù).
ˆC1C1^+ ˆC2C2^=1800 (Hai góc kề bù)
Mà ˆB2B2^=ˆC2C2^(gt)
Nên ˆB1B1^=ˆC1C1^
* ∆ABD và ∆ACE có:
ˆB1B1^=ˆC1C1^(cmt)
BD=EC(gt)
ˆDD^ = ˆEE^(gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
ˆDD^=ˆEE^(gt)
ˆC2C2^=ˆB2B2^(gt)
DC=EB
Nên ∆ADC=∆AEB(g.c.g)

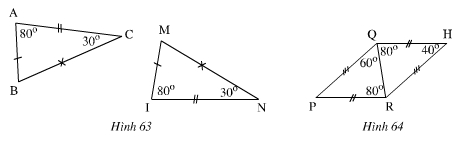
Hình 63
Ta có:
Và AB = MI; AC = IN; BC = MN
Nên ΔABC = ΔIMN
Hình 64 :
ΔPQR có:
Và QH = RP, HR = PQ, QR ( cạnh chung )
Nên ΔHQR = ΔPRQ


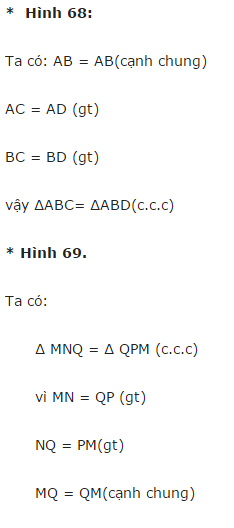
Hình 68.
Xét \(\Delta ABC;\Delta ABD\):
AC = AD (gt)
AB chung
BC = BD (gt)
=> \(\Delta ABC=\Delta ABD\left(c.c.c\right)\)
Hình 69.
Xét \(\Delta MNQ;\Delta QPM:\)
MN = QP (gt)
MQ chung
NQ = PM (gt)
=> \(\Delta MNQ=\Delta QPM\left(c.c.c\right)\)
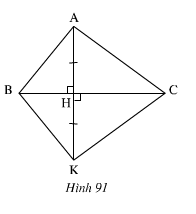
Hình 70. Gọi giao điểm của HK và EI là O.
Xét tg HEI; tg KIE:
EH = KI
EI chung
HI = KE
=> tg HEI = tg KIE (c.c.c)
=> g HEI = g KIE hay g HEO = g OIK
Tương tự: tg HIK = tg KEH (c.c.c)
=> g IHK = g EKH hay g IHO = g OKE
Xét tg HEO; tg KIO:
g HEO = g OIK (c/m trên)
HE = KI
g EHO = g OKI (cộng góc)
=> tg HEO = tg KIO (g.c.g)
Tương tự: tg HIO = tg KEO (g.c.g)


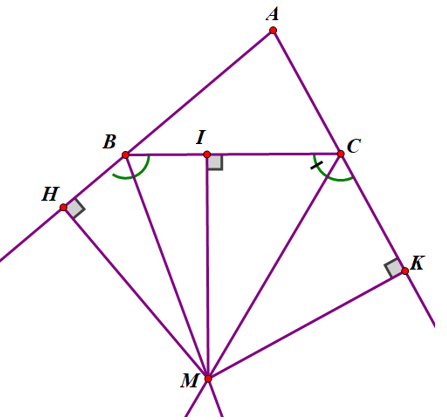
Gọi M là giao điểm của hai tia phân giác của hai góc ngoài B và C của ∆ABC.
Kẻ MH ⊥ AB; MI ⊥ BC; MK ⊥ AC (như hình vẽ)
(H ∈ tia AB, I ∈ BC, K ∈ tia AC)
Theo định lí 1: Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh của góc đó.
Ta có: MH = MI (Vì M thuộc phân giác của góc B ngoài )
MI = MK ( Vì M thuộc phân giác của góc C ngoài )
Suy ra: MH = MK (cùng bằng MI)
Dựa vào định lí 2: Điểm nằm bên trong góc và cách đều hai cạnh của góc thì nằm trên tia phân giác của góc đó.
⇒ M thuộc phân giác của góc BAC (đpcm).
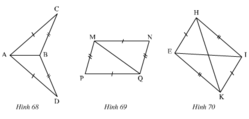




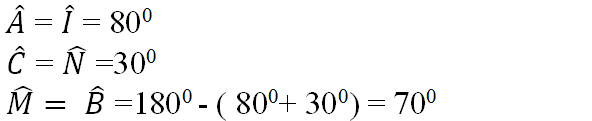
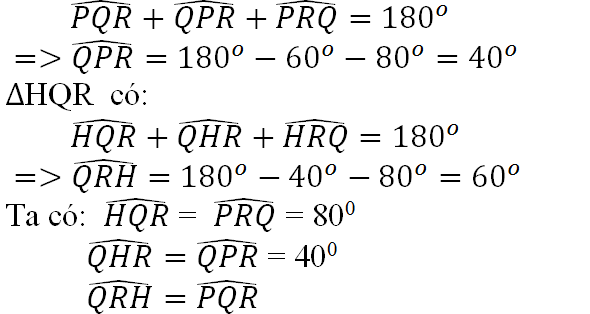

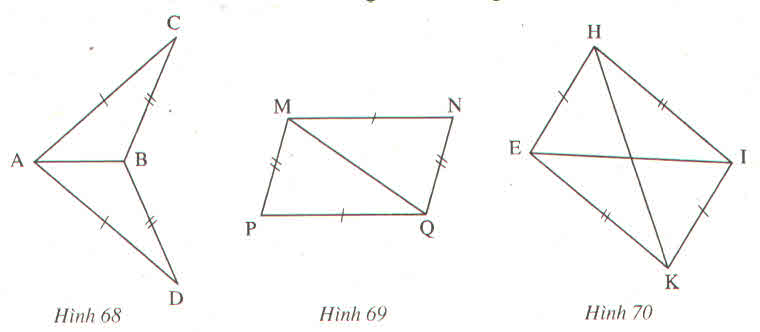








- Hình 68
Xét tam giác ABC và tam giác ABD có:
AB = AB (cạnh chung)
AC = AD (gt)
BC = BD (gt)
Vậy ΔABC = ΔABD (c.c.c)
- Hình 69
Xét tam giác MNQ và tam giác QPM có:
MN = QP (gt)
NQ = PM (gt)
MQ cạnh chung
Vậy ΔMNQ = ΔQPM (c.c.c)
- Hình 70
Xét tam giác EHI và tam giác IKE có:
EH = IK (gt)
HI = KE (gt)
EI = IE (cạnh chung)
Vậy ΔEHI = ΔIKE (c.c.c)
Xét tam giác EHK và tam giác IKH có:
EH = IK (gt)
EK = IH (gt)
HK = KH (cạnh chung)
Vậy ΔEHK = ΔIKH (c.c.c)