Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1: Tọa độ A là:
y=0 và 4x+m-3=0
=>x=(-m+3)/4 và y=0
=>OA=|m-3|/4
Tọa độ B là:
x=0 và y=m-3
=>OB=|m-3|
Theo đề, ta có: 1/2*(m-3)^2/4=9
=>(m-3)^2/4=18
=>(m-3)^2=72
=>\(m=\pm6\sqrt{2}+3\)
2:
PTHĐGĐ là:
x^2-4x-m+3=0
Δ=(-4)^2-4*(-m+3)=16+4m-12=4m+4
Để (P) cắt (d) tại hai điểm phân biệt thì 4m+4>0
=>m>-1
(4-x1)(x2-1)=2
=>4x2-4-x1x2+1=2
=>x2(x1+x2)-3-(-m+3)=2
=>x2*4-3+m-3=2
=>x2*4=2-m+6=8-m
=>x2=2-1/2m
=>x1=4-2+1/2m=1/2m+2
x1*x2=-m+3
=>-m+3=(1/2m+2)(2-1/2m)=4-1/4m^2
=>-m+3-4+1/4m^2=0
=>1/4m^2-m-1=0
=>m^2-4m-4=0
=>\(m=2\pm2\sqrt{2}\)
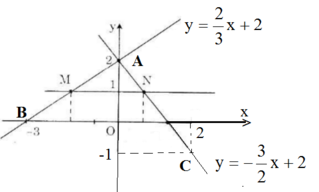
b) Điểm M có tung độ y = 1 nên hoành độ là
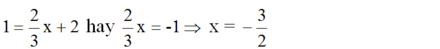
Điểm N có tung độ y = 1 nên hoành độ là
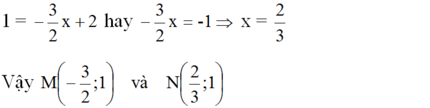
a: Thay y=0 vào (1), ta được:
2x-1=0
hay \(x=\dfrac{1}{2}\)
Thay x=0 vào (1), ta được:
\(y=2\cdot0-1=-1\)
Vậy: \(A\left(\dfrac{1}{2};0\right)\); B(0;-1)
Thay y=0 vào (2), ta được:
x-1=0
hay x=1
Thay x=0 vào (2), ta được:
y=0-1=-1
Vậy: M(1;0); N(0;-1)
??)
cái chỗ có chữ suy ra cũng cần phải chứng minh đó bạn chứ không suy ra thẳng đâu,nhiều khi hắn còn khó hơn vế trước á
Vì OA là tiếp tuyến \(\Rightarrow\angle OAE=\angle OCA\) (góc tạo bởi tiếp tuyến và dây cung bằng góc nội tiếp chắn cung đó)
Xét \(\Delta OAE\) và \(\Delta OCA:\) Ta có: \(\left\{{}\begin{matrix}\angle OAE=\angle OCA\\\angle AOCchung\end{matrix}\right.\)
\(\Rightarrow\Delta OAE\sim\Delta OCA\left(g-g\right)\Rightarrow\dfrac{OA}{OC}=\dfrac{OE}{OA}\Rightarrow OA^2=OC.OE\)
\(\Delta OAE\sim\Delta OCA\Rightarrow\dfrac{AE}{AC}=\dfrac{OA}{OC}\)
Tương tự \(\Rightarrow\Delta OBE\sim\Delta OCB\left(g-g\right)\Rightarrow\dfrac{BE}{BC}=\dfrac{OB}{OC}\)
mà \(OB=OA\) (tính chất tiếp tuyến) \(\Rightarrow\dfrac{BE}{BC}=\dfrac{AE}{AC}\Rightarrow AC.BE=AE.BC\)
a: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x-1=-x+3\\y=x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
a) Vẽ đồ thị:
b) - Từ hình vẽ ta có: yA = yB = 4 suy ra:.
+ Hoành độ của A: 4 = 2.xA => xA = 2 (*)
+ Hoành độ của B: 4 = xB => xB = 4
=> Tọa độ 2 điểm là: A(2, 4); B(4, 4)
- Tìm độ dài các cạnh của ΔOAB
((*): muốn tìm tung độ hay hoành độ của một điểm khi đã biết trước hoành độ hay tung độ, ta thay chúng vào phương trình đồ thị hàm số để tìm đơn vị còn lại.)
Trên mặt phẳng tọa độ Oxy, cho điểm M(2;5). Khi đó:
A. Đường tròn (M;5) cắt hai trục Ox,Oy.
B. Đường tròn (M;5) cắt trục Ox và tiếp xúc với trục Oy.
C. Đường tròn (M;5) tiếp xúc với trục Ox và cắt trục Oy.
D. Đường tròn (M;5) không cắt cả hai trục Ox,Oy.
Học tốt!