Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Phương pháp: Viết phương trình dao động của phần tử tại M, xét đặc điểm của pha và biên độ.
Cách giải:
Đặt phương trình dao động tại hai nguồn là:
Ta có phương trình dao động của phần tử môi trường tại M là:
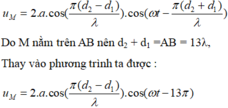
Vậy phần tử tại M luôn dao động ngược pha so với nguồn, cần tìm điều kiện để M cực đại:
Chọn đáp án D.
Không mất tính tổng quát giả sử λ = 1.
Ta có:
Vì trên AB có 11 vị trí cực đại nên suy ra 5 < λ < 6.
(Dựa vào các đáp án suy ra chỉ có 5,3λ thỏa mãn).
Đáp án B
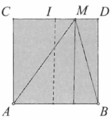
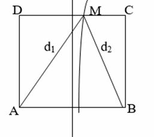
Theo đề, trên AB có 9 vị trí mà ở đó các phần tử nước dao động với biên độ cực đại nên:
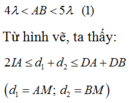
Vì I là trung điểm CD, ABCD là hình vuông nên
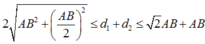
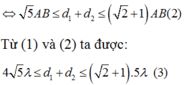
Vì hai nguồn A, B đồng pha nên giả sử:
Lúc đó, phương trình dao động tại điểm M là:
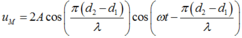
M là cực đại giao thoa bậc nhất:
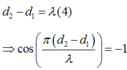
Để M dao động ngược pha với các nguồn thì:
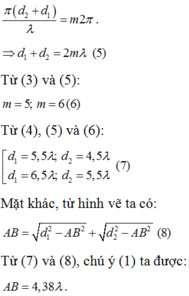
Đáp án B
Điểm M thuộc đoạn AB có phương trình:
(*)
M có biên độ cực đại và cùng pha với nguồn:
Mặc khác 
(1)
và (2) 
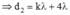với 
→ 
Vậy: 
Có 6 giá trị của k
Đáp án C
Để đơn giản, ta chọn λ = 1 → A B = 6 , 6
Để một điểm trên A C cực đại và cùng pha với nguồn thì d 1 + d 2 = k d 1 + d 2 = n ≥ A B = 6 , 6 . Trong đó n và k có độ lớn cùng chẵn hoặc lẻ
Mặc khác để khoảng cách A C là ngắn nhất thì cos α = A B 2 + d 1 2 − d 2 2 2 A B . d 1 phải lớn nhất
Ta để ý rằng khi xảy ra cực đại thì mỗi bên trung trực của A B có 6 dãy cực đại ứng với k = 1 , ± 2..... ± 6 . Với mỗi giá trị của k ta tìm được cặp giá trị d 1 , d 2
→ Thử các giá trị của k , nhận thấy cos α lớn nhất khi k = 1 và d 1 = 3 d 2 = 4
→ h min = A B 2 tan α ≈ 1 , 3757
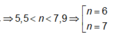
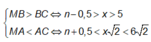
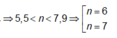
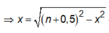
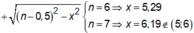
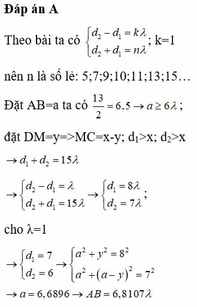
Đáp án D
Phương trinh dao động của điểm M là:
Đến đây chúng ta chú ý:
Để M cực đại thì:
Để M cực đại cùng pha với nguồn thì:
Để M cực đại ngược pha với nguồn thì:
Từ yêu cầu bài toán suy ra: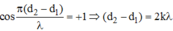
Vậy có 11 giá trị của k thỏa mãn nên có 11 cực đại ngược pha với hai nguồn trên đoạn AB.