Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi phương trình đường thẳng đi qua hai điểm A và B là: y = ax + by = ax+b. A thuộc đường thẳng y = ax + by = ax+b nên: 0.a + b = 2 ⇔ b = 2 0.a+b = 2⇔b = 2. B thuộc đường thẳng y = a x + b y=ax+b nên: ( − 3 ) a + b = 4 (−3)a+b=4 ⇔ a = 4 − b − 3 ⇔a=4−b−3 = 4 − 2 − 3 = − 2 3 =4−2−3=−23. Vậy phương trình đường thẳng AB là: y = − 2 3 x + 2 y=−23x+2. Do − 2 3 .6 + 2 = − 2 −23.6+2=−2 nên C thuộc đường thẳng AB hay A, B, C thẳng hàng.

1:
a: 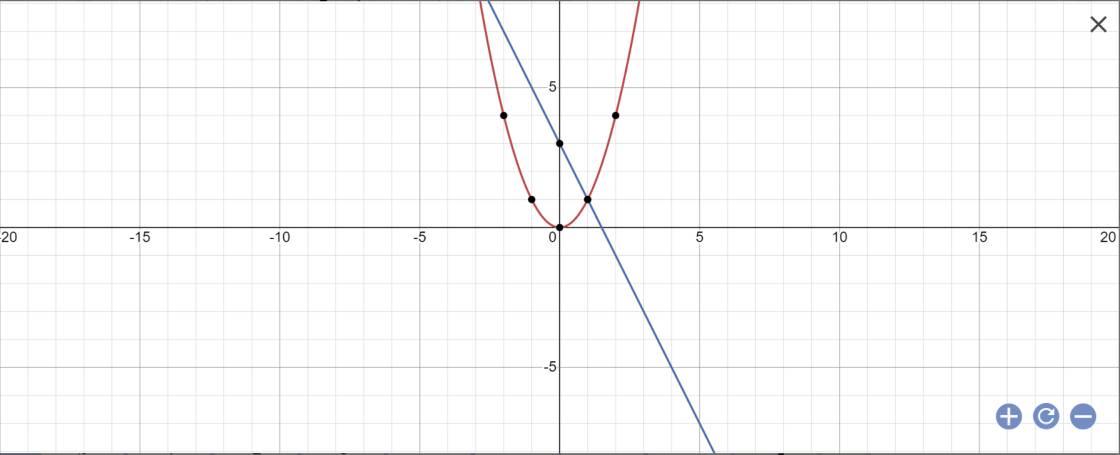
b: PTHĐGĐ là:
x^2+2x-3=0
=>(x+3)(x-1)=0
=>x=-3 hoặc x=1
=>y=9 hoặc y=1

a:
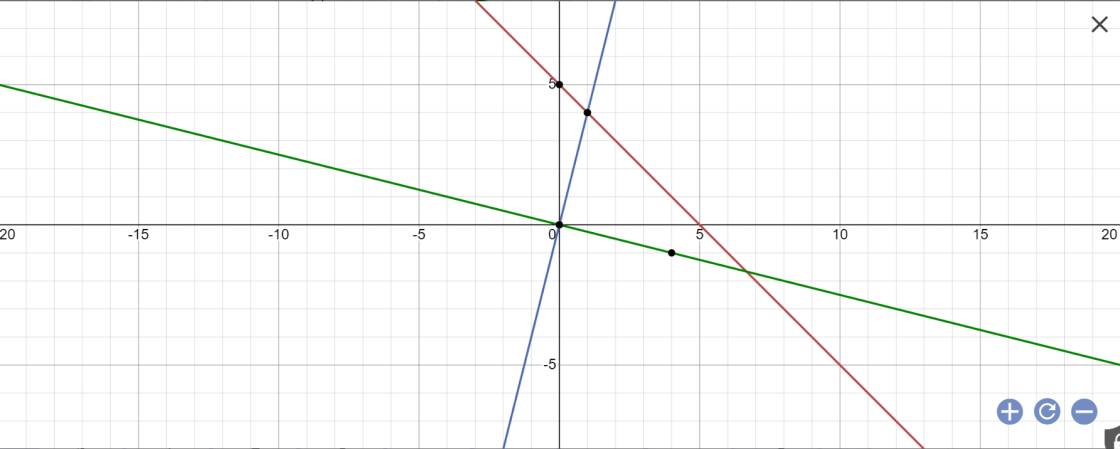
b: tọa độ A là;
-x+5=4x và y=4x
=>x=1 và y=4
Tọa độ B là;
-x+5=-1/4x và y=-1/4x
=>-3/4x=-5 và y=-1/4x
=>x=5:3/4=5*4/3=20/3 và y=-1/4*20/3=-5/3
=>B(20/3;-5/3)
c: O(0;0); A(1;4); B(20/3;-5/3)
\(OA=\sqrt{1^2+4^2}=\sqrt{17}\)
\(OB=\sqrt{\left(\dfrac{20}{3}\right)^2+\left(-\dfrac{5}{3}\right)^2}=\dfrac{5\sqrt{17}}{3}\)
\(AB=\sqrt{\left(\dfrac{20}{3}-1\right)^2+\left(-\dfrac{5}{3}-4\right)^2}=\dfrac{\sqrt{818}}{3}\)
\(cosAOB=\dfrac{OA^2+OB^2-AB^2}{2\cdot OA\cdot OB}=\dfrac{-8}{17}\)
=>góc AOB tù
=>ΔOAB tù

a: 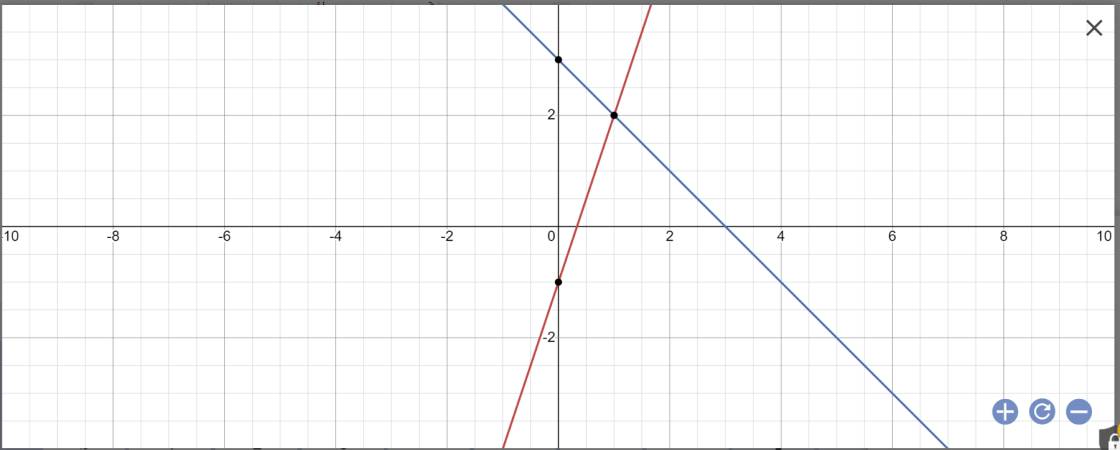
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\3x-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=0\end{matrix}\right.\)
Vậy: A(1/3;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\-x+3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\-x=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=3\end{matrix}\right.\)
Vậy: B(3;0)
Tọa độ C là:
\(\left\{{}\begin{matrix}3x-1=-x+3\\y=3x-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x=4\\y=3x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\cdot1-1=2\end{matrix}\right.\)
Vậy: C(1;2)
c: Gọi \(\alpha\) là góc tạo bởi (d1) với trục Ox
\(tan\alpha=a=3\)
=>\(\alpha\simeq71^033'\)