Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo Cô si 4x+\frac{1}{4x}\ge24x+4x1≥2 , đẳng thức xảy ra khi và chỉ khi 4x=\frac{1}{4x}=1\Leftrightarrow x=\frac{1}{4}4x=4x1=1⇔x=41). Do đó
A\ge2-\frac{4\sqrt{x}+3}{x+1}+2016A≥2−x+14x+3+2016
A\ge4-\frac{4\sqrt{x}+3}{x+1}+2014A≥4−x+14x+3+2014
A\ge\frac{4x-4\sqrt{x}+1}{x+1}+2014=\frac{\left(2\sqrt{x}-1\right)^2}{x+1}+2014\ge2014A≥x+14x−4x+1+2014=x+1(2x−1)2+201

a: Tọa độ A là:
y=0 và -2x+2=0
=>x=1 và y=0
=>A(1;0)
Tọa độ B là:
x=0 và y=-2x+2
=>x=0 và y=-2*0+2=2
=>B(0;2)
b: C thuộc Ox nên C(x;0)
D thuộc Oy nên D(0;y)
ABCD là hình thoi nên AB=AD và vecto AB=vecto DC
A(1;0); B(0;2); C(x;0); D(0;y)
\(\overrightarrow{AB}=\left(-1;2\right);\overrightarrow{DC}=\left(x;-y\right)\)
\(AB=\sqrt{\left(0-1\right)^2+\left(2-0\right)^2}=\sqrt{5}\)
\(AD=\sqrt{\left(0-1\right)^2+\left(y-0\right)^2}=\sqrt{y^2+1}\)
vecto AB=vecto DC
=>x=-1 và -y=2
=>x=-1 và y=-2
AB=AD
=>y^2+1=5
=>y^2=4
=>y=2(loại) hoặc y=-2(nhận)
Vậy: x=-1 và y=-2
=>C(-1;0); D(0;-2)
Gọi phương trình (d2) có dạng là y=ax+b
(d2) đi qua C và D nên ta có hệ phương trình:
a*(-1)+b=0 và 0*a+b=-2
=>b=-2 và -a=-b=2
=>a=-2 và b=-2
=>y=-2x-2
c: (d1): y=-2x+2 và (d2): y=-2x-2
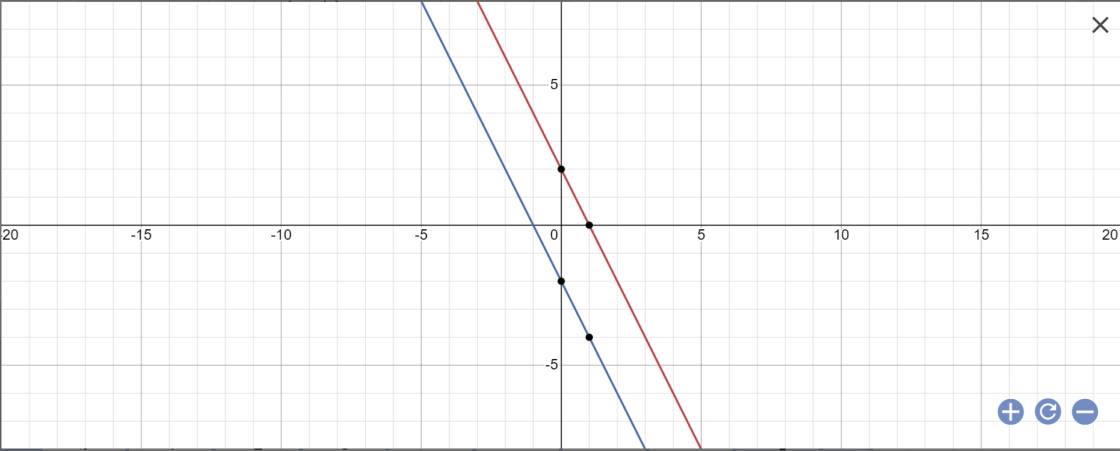

a/ \(\left\{{}\begin{matrix}a+b=3\\-3a+b=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)
b/ \(\left\{{}\begin{matrix}a=3\\2a+b=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=3\\b=-4\end{matrix}\right.\)
c/ \(\left\{{}\begin{matrix}a=-2\\2a+b=-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-2\\b=1\end{matrix}\right.\)
d/ \(\left\{{}\begin{matrix}a.3=-1\\-2a+b=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\frac{1}{3}\\b=\frac{1}{3}\end{matrix}\right.\)
e/ \(\left\{{}\begin{matrix}a=-2\\a+b=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-2\\b=2\end{matrix}\right.\)

a/ \(\left\{{}\begin{matrix}a+b=3\\-3a+b=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=1\\b=2\end{matrix}\right.\)
b/ \(\left\{{}\begin{matrix}a=3\\2a+b=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=3\\b=-4\end{matrix}\right.\)
c/ \(\left\{{}\begin{matrix}a=-2\\2a+b=-3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-2\\b=1\end{matrix}\right.\)
d/ \(\left\{{}\begin{matrix}a.3=-1\\-2a+b=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\frac{1}{3}\\b=\frac{1}{3}\end{matrix}\right.\)
e/ \(\left\{{}\begin{matrix}a=-2\\a.1+b=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-2\\b=2\end{matrix}\right.\)

a, Đường thẳng d cắt trục hoành tại điểm có hoành độ bằng 2 nên
( d ) đi qua A( 2,0 )
Thay A( 2,0 ) vào đường thẳng d ta được
\(\left(1-m\right).2+m+2=0\)
\(2-2m+m+2=0\)
\(4-m=0\)
\(m=4\)
b, Đường thẳng d song song vs đường thẳng y = 2x - 1 nên
1 - m = 0 và m + 2 khác -1
m = 1 và m khác -3




a/ \(\left\{{}\begin{matrix}2a+b=1\\5a+b=-\frac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\frac{1}{2}\\b=2\end{matrix}\right.\)
b/ Theo câu a, ta có pt MN là: \(y=-\frac{1}{2}x+2\)
Giao điểm của MN với Ox:
\(y=0\Rightarrow-\frac{1}{2}x+2=0\Rightarrow x=4\Rightarrow A\left(4;0\right)\)
Giao điểm MN với trục Oy:
\(x=0\Rightarrow y=2\Rightarrow B\left(0;2\right)\)