Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E F H G L M N P
Độ dài chiều rộng của hình chữ nhật ABCD là:
20 + 40 = 60 (m)
Độ dài chiều dài của hình chữ nhật ABCD là:
40 + 10 + 35 = 85 (m)
Diện tích hình chữ nhật ABCD là:
60 . 85 = 5100 (m2).
Diện tích tam giác vuông HEN là:
\(\dfrac{10.20}{2}\)= \(\dfrac{200}{2}=100\left(m^2\right)\)
Diện tích tam giác vuông AHG là:
\(\dfrac{20.40}{2}=\dfrac{800}{2}=400\left(m^2\right)\)
Diện tích tam giác vuông MLP là:
\(\dfrac{15.50}{2}=\dfrac{750}{2}=375\left(m^2\right)\)
Diện tích hình thang vuông EBNF là:
\(\dfrac{\left(20+35\right).35}{2}=\dfrac{1925}{2}=962,5\left(m^2\right)\)
Diện tích hình thang vuông GMCL là:
\(\dfrac{\left(40+15\right).15}{2}=\dfrac{825}{2}=412,5\left(m^2\right)\)
Tổng diện tích các hình nằm ngoài hình gạch sọc và nằm trong hình chữ nhật ABCD là:
100 + 400 + 375 + 962,5 + 412,5 = 2250 (m2).
Diện tích hình sọc dọc là:
5100 - 2250 = 2850 (m2).
Vậy diện tích hình sọc dọc là 2850m2.

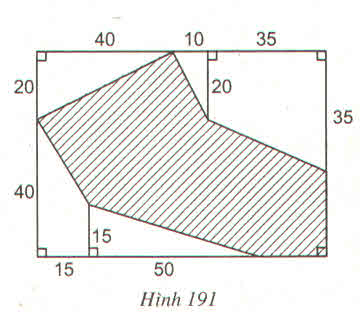
Ta có:
SABCD=(40+10+35).(20+40) = 5100 (cm2)
S1=\(\dfrac{40.20}{2}=400\left(cm^2\right)\)
S2=\(\dfrac{10.20}{2}=100\left(cm^2\right)\)
S3=\(\dfrac{\left(20+35\right).35}{2}=962,5\left(cm^2\right)\)
S4=\(\dfrac{50.15}{2}=375\left(cm^2\right)\)
S5=\(\dfrac{\left(15+40\right).15}{2}=412,5\left(cm^2\right)\)
=> Shình gạch sọc= S - ( S1+S2+S3+S4+S5)= 5100-(400+100+962,5+375+412,5)=2850(cm2)


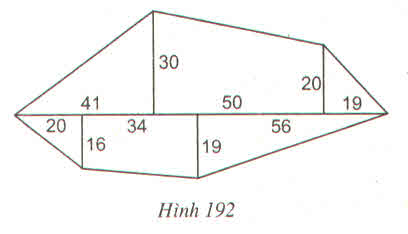
S1=\(\dfrac{30.41}{2}=615\left(cm^2\right)\)
S2=\(\dfrac{\left(30+20\right).50}{2}=1250\left(cm^2\right)\)
S3=\(\dfrac{19.20}{2}=190\left(cm^2\right)\)
S4=\(\dfrac{19.56}{2}=532\left(cm^2\right)\)
S5=\(\dfrac{\left(19+16\right).34}{2}=595\left(cm^2\right)\)
S6=\(\dfrac{16.20}{2}=160\left(cm^2\right)\)
=> S= S1 + S2 +S3 +S4 +S5 +S6= 615+1250+190+532+595+160=3342(m2)

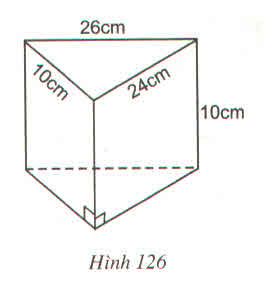
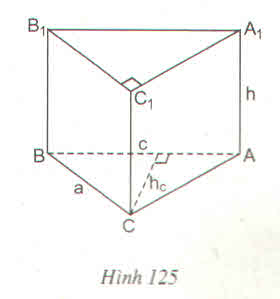
Diện tích đáy lăng trụ là:
\(S=\dfrac{1}{2}\cdot2x=x\left(cm^2\right)\)
\(V=S\cdot h\)
=>x=V/h=3(cm)

ABA′B′ABA′B′ = BCB′C′BCB′C′= CAC′A′CAC′A′= 3/2
=> ∆ABC ∽ ∆A'B'C'
b) CABCCA′B′C′CABCCA′B′C′= 3/2
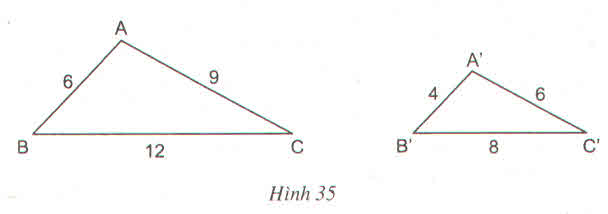
a)Xét \(\Delta ABC\) và \(\Delta A'B'C'\) có:
\(\dfrac{AB}{A'B'}=\dfrac{BC}{B'C'}=\dfrac{AC}{A'C'}\)
\(\Rightarrow\Delta ABC\)∽\(\Delta A'B'C'\)(c.c.c)
b)Từ câu a và áp dụng tính chất tỉ lệ thức ta có:
\(\dfrac{AB}{A'B'}=\dfrac{BC}{B'C'}=\dfrac{AC}{A'C'}=\dfrac{AB+BC+AC}{A'B'+B'C'+A'C'}=\dfrac{3}{2}\)
mà \(C_{ABC}=AB+BC+AC\)
\(C_{A'B'C'}=A'B'+B'C'+A'C'\)
Vậy tỉ số chu vi của \(\Delta ABC\) và \(\Delta A'B'C'\)là:
\(\dfrac{C_{ABC}}{C_{A'B'C'}}=\dfrac{3}{2}\)

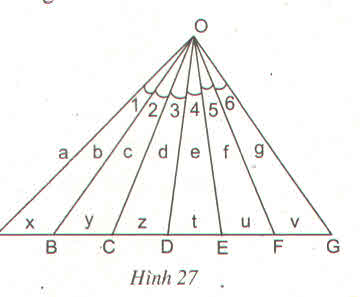
Giải
OB là tia phân giác trong của ∆OBC => xaxa = ycyc
OC là tia phân giác trong của ∆OBD => ydyd = zdzd
OD là tia phân giác trong của ∆OCE => zczc = tete
OE là tia phân giác trong của ∆ODF => tdtd = ufuf
OC là tia phân giác của ∆ACE => OCOAOCOA = CEOECEOE hay x+yax+ya = z+tez+te
OE là phân giác của ∆OCG => z+tcz+tc = u+vgu+vg
OD là phân giác của ∆AOG => x+y+xax+y+xa = t+u+vgt+u+vg
OD là phân giác của ∆OBF => y+zby+zb = t+uf

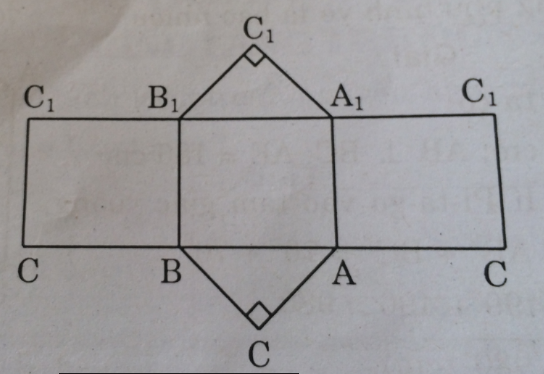
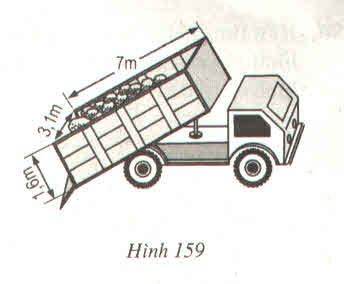
\(a,\) Thùng chứa có dạng một lăng trụ đứng
V= 1,6.3,1.7=34,72 (m3)
\(b,\) Cát nặng :
\(34,72.\dfrac{3}{4}.1,6=41,664\) (tấn)





Chu vi mỗi hình lần lượt là: ( 6+1).2 = 14 và ( 3+ 2).2 = 10 ( đơn vị).
Diện tích hai hình bằng nhau và bằng: 6.1 = 3.2= 6 ( đơn vị diện tích) .