K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
30 tháng 9 2018
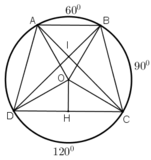
+ ∆ O A B có

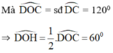
∆ O D H vuông, áp dụng hệ thức về cạn và góc trong tam giác vuông ta có
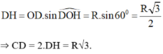

CM
11 tháng 8 2019
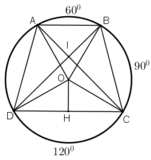


=> AB//CD (hai góc trong cùng phía bù sau)
=> ABCD là hình thang.

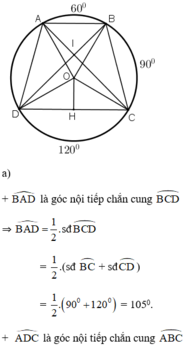



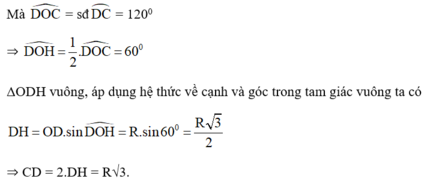

ˆBAD=900+12002=1050BAD^=900+12002=1050 (góc nội tiếp chắn cung BCD) (1)
ˆADC=600+9002=750ADC^=600+9002=750 ( góc nội tiếp chắn cung ABC) (2)
Từ (1) và (2) có:
ˆBAD+ˆADC=1050+750=1800BAD^+ADC^=1050+750=1800 (3)
ˆBADBAD^ và ˆADCADC^ là hai góc trong cùng phía tạo bởi cát tuyến AD và hai đường thẳng AB, CD.
Đẳng thức (3) chứng tỏ AB // CD. Do đó tứ giác ABCD là hình thang, mà hình thang nội tiếp là hình thang cân.
Vậy ABCD là hình thang cân (BC = AD và sđ cung BC = AD = 90o )
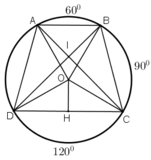
b) Giả sử hai đường chéo AC và BD cắt nhau tại I.
ˆCIDCID^ là góc có đỉnh nằm trong đường tròn, nên:
ˆCID=sđcungAB+sđcungCD2=600+12002=900CID^=sđcungAB+sđcungCD2=600+12002=900
Vậy AC ⊥ BD
c)
Vì sđ cung AB = 60o nên ˆAIB=600AIB^=600 => ∆AIB đều, nên AB = R
Vì sđ cung BC = 90o nên BC = R√2
AD = BC = R√2
nên sđ cung CD= 120o nên CD = R√3
Hướng dẫn giải:
ˆBAD=900+12002=1050BAD^=900+12002=1050 (góc nội tiếp chắn cung BCD) (1)
ˆADC=600+9002=750ADC^=600+9002=750 ( góc nội tiếp chắn cung ABC) (2)
Từ (1) và (2) có:
ˆBAD+ˆADC=1050+750=1800BAD^+ADC^=1050+750=1800 (3)
ˆBADBAD^ và ˆADCADC^ là hai góc trong cùng phía tạo bởi cát tuyến AD và hai đường thẳng AB, CD.
Đẳng thức (3) chứng tỏ AB // CD. Do đó tứ giác ABCD là hình thang, mà hình thang nội tiếp là hình thang cân.
Vậy ABCD là hình thang cân (BC = AD và sđ cung BC = AD = 90o )
b) Giả sử hai đường chéo AC và BD cắt nhau tại I.
ˆCIDCID^ là góc có đỉnh nằm trong đường tròn, nên:
ˆCID=sđcungAB+sđcungCD2=600+12002=900CID^=sđcungAB+sđcungCD2=600+12002=900
Vậy AC ⊥ BD
c)
Vì sđ cung AB = 60o nên ˆAIB=600AIB^=600 => ∆AIB đều, nên AB = R
Vì sđ cung BC = 90o nên BC = R√2
AD = BC = R√2
nên sđ cung CD= 120o nên CD = R√3