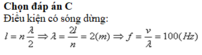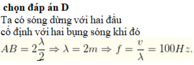Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bước sóng: \(\lambda=\dfrac{v}{f}=\dfrac{20}{40}=0,5m\)
Hai đầu A và B cố định.
a)Số bụng sóng: \(l=k\cdot\dfrac{\lambda}{2}\Rightarrow1=k\cdot\dfrac{0,5}{2}\Rightarrow k=4\)
b)Số nút sóng là: \(nút=k+1=4+1=5\)
c)Tổng số bụng và nút sóng là: \(4+5=9\)

Đáp án A
+ Điều kiện để có sóng dừng trên dây với hai đầu cố định l = n v 2 f với n là số bó sóng trên dây.
→ n = 2 l f v = 2 . 1 , 2 . 30 24 = 3 → trên dây có 3 bụng và 4 nút.

Sóng dừng trên dây có 2 đầu cố định thì tần số cơ bản \(f_0\) (tần số nhỏ nhất để có sóng dừng ứng với 1 bó sóng)
Thì các tần số để có sóng dừng là: \(f_n=n.f_0\)
Suy ra: \(f_0=8Hz\)
Có: \(\dfrac{1}{\lambda_{n+1}}-\dfrac{1}{\lambda_{n}}=\dfrac{f_{n+1}}{v}-\dfrac{f_{n}}{v}=\dfrac{8}{v}=0,2\Rightarrow v=40m/s\)
Tần số âm cơ bản ứng với 1 bó sóng ta có: \(l=\dfrac{\lambda}{2}=\dfrac{v}{2f_0}=\dfrac{40}{2.8}=2,5m\)
Chọn D.

Áp dụng điều kiện có sóng dừng trên sợi dây có hai đầu cố định ta có
l = n λ /2 = nv/2f ⇒ n = 2fl/v = 2.40.1/20 = 4 bụng
⇒ 5 nút.

a)\(U_M=2Acos\left(\pi\frac{\left(d_2-d_1\right)}{\lambda}\right)\) \(cos\left(\omega t-\pi\frac{d_1+d_2}{\lambda}\right)\)
thay số vào ta đc
\(U_M=\frac{\sqrt{2}}{2}cós\left(20\pi t-\frac{29\pi}{4}\right)\)
b) số cực đại \(\frac{-AB}{\lambda}\le n\le\frac{AB}{\lambda}\)
nên \(-2,75\le n\le2,75\)
có 5 giá trị n nguyên, vậy số cực đại là 5
số cực tiểu \(\frac{-AB}{\lambda}-\frac{1}{2}\le n\le\frac{AB}{2}-\frac{1}{2}\)
thay số tương tự nhé
ừ thì bước sóng bằng 8cm đúng rồi
còn d2 với d1 thì k quan trọng đâu, lấy cái nào trừ cái nào cũng đc