Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Không thể khẳng định câu trên là đúng hay sai.
b)
+) n = 0 hoặc n =5 thì “n chia hết cho 5” là khẳng định đúng.
+) n = 2 hoặc n =34 thì “n chia hết cho 5” là khẳng định sai.

a) Ta chưa thể khẳng định được tính đúng sai của câu “n chia hết cho 3” do chưa có giá trị cụ thể của n.
b) Với n = 21 thì câu ”21 chia hết cho 3” là mệnh đề toán học. Mệnh đề này đúng.
c) Với n = 10 thì câu ”10 chia hết cho 3” là mệnh đề toán học. Mệnh đề này sai.

D sai, vì hệ số góc $a=1>0$, khi $x$ tăng (giảm) thì $y$ tương ứng tăng (giảm) nên hàm đồng biến trên $R$

Đáp án D
Ta có thể thấy ngay rằng các khẳng định A và C đều đúng.
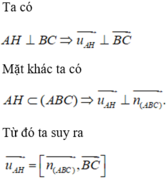
là một vectơ chỉ phương của đường thẳng AH.
Vậy D là khẳng định sai.

Ta có tập nghiệm của phương trình là:
\(\left(x+2\right)\left(2x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+2=0\\2x-1=0\\x-3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\2x=1\\x=3\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{1}{2}\\x=3\end{matrix}\right.\)
Tập hợp S là:
\(S=\left\{-2;\dfrac{1}{2};3\right\}\)
Lần lược các phương án:
A. \(-2\in S\) (đúng)
B. \(3\in S\) (đúng)
C. \(2\in S\) (Sai)
D. \(\dfrac{1}{2}\in S\) (Đúng)
⇒ Chọn C

a) Phát biểu của bạn H’Maryam là một câu khẳng định về tính chất chia hết trong toán học.
b) Phát biểu của bạn phương không phải là một câu khẳng định về một sự kiện trong toán học.

Vì sao trong trường hợp cả 2024 câu đã là đúng thì chính chúng lại là những câu sai ạ? Nếu vậy thì nó vô lý rồi ạ, vì một mệnh đề không thể vừa đúng vừa sai được.
Ta loại câu số 2024 vì nếu đây là khẳng định đúng thì số khẳng định sai nhiều nhất chỉ là 2023, không thể có tới 2024 khẳng định sai.
Xét câu 1: nếu có ít nhất 1 câu khẳng định sai thì khẳng định sai là câu 2024. Vậy thì câu 2 sẽ đúng, tuy nhiên câu thứ 2 mâu thuẫn với câu 1, vậy câu 1 sai.
Xét câu \(n\left(1< n< 2023\right)\), nếu có ít nhất n câu khẳng định sai thì khẳng định sai là câu \(1,...,n-1,2024\), Vậy thì câu \(n+1\) sẽ đúng, tuy nhiên câu thứ \(n+1\) mâu thuẫn với câu n, vậy câu n sai.
Sau khi loại từ câu 1 tới 2022 và câu 2024. Ta thấy có 2023 khẳng định sai, vậy câu 2023 đúng.