

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




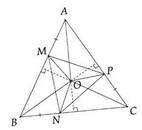
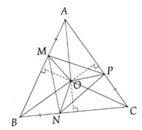
a, Vì \(\Delta ABC\) đều và \(O\) là giao điểm 3 đường trung trực nên \(AO\) là tia phân giác của \(\widehat{A}\)
\(\Rightarrow\widehat{MAO}=\dfrac{\widehat{BAC}}{2}=30^o\)
b, Tương tự a, \(\widehat{OCB}=30^o\)
Chứng minh được: \(\Delta MAO=\Delta OPC\left(c.g.c\right)\)
Ta có: \(\Delta MAO=\Delta OPC\Rightarrow OM=OP\left(1\right)\)
c, Tương tự b
\(\Delta MAO=\Delta NBO\left(c.g.c\right)\)
\(\Rightarrow ON=OM\left(2\right)\)
Từ (1) và (2) suy ra O là giao điểm
3 đương trung trực của tam giác MNP

a: góc OAM=60/2=30 độ
b; Xét ΔOAM và ΔCPO có
OA=OC
góc OAM=gócPCO
AM=CP
=>ΔOAM=ΔCPO