Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Thời gian người thứ hai đến điểm 780m là :
t2 = \(\frac{780}{1,9}\) \(\approx\) 410,5 s
b) 5,50 phút = 300giây + 30giây = 330giây
Gọi t là thời gian người thứ 2 đi => (t+330) là thời gian người thứ nhất đi
Quãng đường người thứ nhất đi: S = 0,9(t+330)
Quãng đường người thứ hai đi: S = 1,9t
=> S = 0,9(t+330) = 1,9t
Ta có phuơng trình: 0,9(t+330)=1,9t; giải hệ có t = 297giây
Vậy vị trí đó cách nơi xuất phát : S =1,9t = 1,9.297 = 564,3m
a) Chọn trục tọa độ trùng với dường thẳng chuyển động , gốc tọa độ là vị trí xuất phát , chiều dương là chiều chuyển động , gốc thời gian là thời điểm xuất phát .
v = \(\frac{\triangle x}{\triangle t}\) → \(\triangle t=\frac{\triangle x}{v}=\frac{780}{1,9}=410,53\left(s\right)=6,84min\) = 6 min 50( s )
b) Gọi t là thời gian người thứ 2 đi cho đến khi dừng lại . Quãng đường người thứ 2 đi được là : S = vt = 1,9t
Cùng trong thời gian t ( s ) , người thứ nhất đi được là : S1 = v1t = 0,9t
Quãng đường người thứ nhất đi được kể từ khi người thứ 2 dừng cho tới lúc gặp nhau là : S2 = v1t` = 0,9 . ( 5,5 . 60 ) 297 ( m )
Ta có : S1 + S2 = S ↔ 297 + 0,9t = 1,9t → t = 297 ( s )
Suy ra : S = 1,9t = 1,9 . 297 = 564,3 ( m )
Vậy vị trí người thứ hai nghỉ cách nơi xuất phát là 564,3 ( m ).

Giải:
a. Chọn chiều dương là chiều chuyển động của xe đạp nhứ nhất gốc tọa độ tại vị trí xe đạp thứ nhất có vận tốc đầu là 4,5km/h, gốc thời gian là lúc hai xe khởi hành.
Đối với xe đạp thứ nhất:



a. Chọn chiều dương là chiều chuyển động của xe đạp nhứ nhất gốc tọa độ tại vị trí xe đạp thứ nhất có vận tốc đầu là 4,5km/h, gốc thời gian là lúc hai xe khởi hành.
Đối với xe đạp thứ nhất:

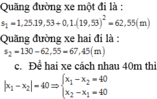
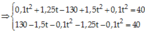
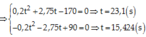

Chọn đáp án B
+ Chọn chiều dương là chiều chuyển động của xe đạp nhứ nhất gốc tọa độ tại vị trí xe đạp thứ nhất có vận tốc đầu là 4,5km/h, gốc thời gian là lúc hai xe khởi hành
+ Đối với xe đạp thứ nhất:


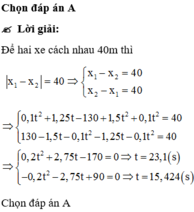



quá dễ cho 1 cuộc tình, my name is tình :)))
Giải như sau:
Ta thấy như sau \(\left\{{}\begin{matrix}x_1=8t\\x_2=10\left(t-\dfrac{1}{4}\right)\\x_3=v\left(t-\dfrac{3}{4}\right)\end{matrix}\right.\)
Khi đuổi kịp thì
+) \(x_3=x_1\Leftrightarrow8t=v\left(t-\dfrac{3}{4}\right)\Rightarrow t=\dfrac{\dfrac{3}{4}v}{\left(v-8\right)}\)
\(\Rightarrow x_A=\dfrac{8\cdot\dfrac{3}{4}v}{v-8}=\dfrac{6v}{v-8}\)
+) \(x_3=x_2\Leftrightarrow10\left(t-\dfrac{1}{4}\right)=v\cdot t-\dfrac{3}{4}v\Rightarrow t=\dfrac{\dfrac{3}{4}v-2,5}{v-10}\)
\(\Rightarrow x_B=\dfrac{5v}{v-10}\)
Có 2 trường hợp \(\left\{{}\begin{matrix}x_A-x_B=5\\x_A-x_B=-5\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}PTVN\\\left[{}\begin{matrix}v=5\left(loại\right)\\v\simeq13,33\left(chọn\right)\end{matrix}\right.\end{matrix}\right.\)
Vậy vận tốc xe 3 là 13,33 (km/h)
.