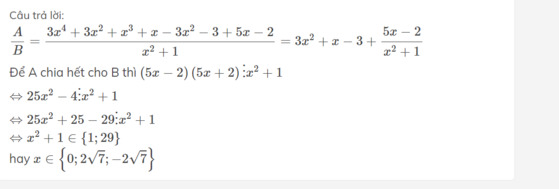Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{A}{B}=\dfrac{3x^4+3x^2+x^3+x-3x^2-3+5x-2}{x^2+1}=3x^2+x-3+\dfrac{5x-2}{x^2+1}\)
Để A chia hết cho B thì \(\left(5x-2\right)\left(5x+2\right)⋮x^2+1\)
\(\Leftrightarrow25x^2-4⋮x^2+1\)
\(\Leftrightarrow25x^2+25-29⋮x^2+1\)
\(\Leftrightarrow x^2+1\in\left\{1;29\right\}\)
hay \(x\in\left\{0;2\sqrt{7};-2\sqrt{7}\right\}\)

Bài 2:
a)\(x^3-2x^2+x\)
\(=x\left(x^2-2x+1\right)\)
\(=x\left(x-1\right)^2\)
b)\(x^2-2x-15\)
\(=x^2-5x+3x-15\)
\(=x\left(x-5\right)+3\left(x-5\right)\)
c)\(y\left(x-z\right)+7\left(z-x\right)\)
\(=7\left(z-x\right)-y\left(z-x\right)\)
\(=\left(7-y\right)\left(z-x\right)\)
\(=\left(x-5\right)\left(x+3\right)\)
d)\(36-12x+x^2\)
\(=x^2-12x+36\)
\(=\left(x-6\right)^2\)
Bài 1:
a)\(2x\left(x^2-7x-3\right)=2x^3-14x^2-6x\)
b)\(\left(-2x^3+34y^2-7xy\right)\cdot4xy^2=136xy^4-28x^2y^3-8x^4y^2\)
c)\(\left(x^2-2x+3\right)\left(x-4\right)\)
\(=x^2\left(x-4\right)-2x\left(x-4\right)+3\left(x-4\right)\)
\(=x^3-4x^2-2x^2+8x+3x-12\)
\(=x^3-6x^2+11x-12\)
d)\(\left(2x^3-3x-1\right)\left(5x+2\right)\)
\(=5x\left(2x^3-3x-1\right)+2\left(2x^3-3x-1\right)\)
\(=10x^4-15x^2-5x+4x^3-6x-2\)
\(=10x^4+4x^3-15x^2-11x-2\)

Phần I
Câu 1: c,d
Câu 2: e
Phần II
Câu 1:
a, 2008a2-2008b2=2008(a2-b2)=2008(a-b)(a+b)
b, x2-8x+15=x2-3x-5x-+15=x(x-3)-5(x-3)=(x-5)(x-3)
Câu 2:
a, M= (x-3)(x+3)-(x+2)2-2(x2-4,5)
M= x2-9-(x2+4x+4)-2x2+9
M= x2-9-x2-4x-4-2x2+9
M= -2x2-4x-4
M= -2(x2+2x+2)b, Để M=0 -> -2(x2+2x+2)=0->x2+2x+2=0
Phần 1:
Câu 1: D
Câu 2: E
Phần 2:
Câu 1:
\(A=2008a^2-2008b^2\)
\(=2008\left(a^2-b^2\right)\)
\(=2008\left(a-b\right)\left(a+b\right)\)
\(B=x^2-8x+15\)
\(=x^2-3x-5x+15\)
\(=x\left(x-3\right)-5\left(x-3\right)\)
\(=\left(x-3\right)\left(x-5\right)\)
Câu 2:
\(M=\left(x-3\right)\left(x+3\right)-\left(x+2\right)^2-2\left(x^2-4,5\right)\)
\(=x^2-9-x^2-4x-4-2x^2+9\)
\(=-2x^2-4x-4\)
\(=-2\left(x^2+2x+2\right)\)
\(=-2\left[\left(x^2+2x+1\right)+1\right]\)
\(=-2\left[\left(x+1\right)^2+1\right]\)
\(=-2-2\left(x+1\right)^2\le-2< 0\)
Vậy không có giá trị nào của x thoả mãn yêu cầu.

Bài 1:
1 (x+3)2=x2+6x+9
2
a, 2x2(3x-5x3)+10x5-5x3=6x3-10x5+10x5-5x3=x3
b, (x+3)(x2-3x+9)+(x-9)(x+3)=(x3+27)+(x2-6x-27)=x3+x2-6x
Bài 2:
a, x2-25x=0
\(\Leftrightarrow x\left(x-25\right)=0\)
\(\Leftrightarrow\begin{cases}x=0\\x-25=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x=0\\x=25\end{cases}\)
b, (4x-1)2-9=0
\(\Leftrightarrow\left(4x-1-3\right)\left(4x-1+3\right)=0\)
\(\Leftrightarrow\left(4x-4\right)\left(4x+2\right)=0\)
\(\Leftrightarrow4\left(x-1\right)2\left(2x+1\right)=0\)
\(\Leftrightarrow8\left(x-1\right)\left(2x+1\right)=0\)
\(\Leftrightarrow\begin{cases}x-1=0\\2x+1=0\end{cases}\)
\(\Leftrightarrow\begin{cases}x=1\\x=\frac{-1}{2}\end{cases}\)
Bài 3:
a, 3x2-18x+27=3(x2-6x+9)=3(x-3)2
b, xy-y2-x+y=y(x-y)-(x-y)=(y-1)(x-y)
c, x2-5x-6=x2-6x+x-6=x(x-6)+(x-6)=(x+1)(x-6)
Bài 4:
a, ( 12x3y3-3x2y3+4x2y4):6x2y3=(12x3y3:6x2y3)-(3x2y3:6x2y3)+(4x2y4:6x2y3)
=2x-1/2 + 2/3y
b, bạn ơi mình không biết cách vẽ đường kẻ để chia ý , nếu bạn biết thì chỉ cho mình rồi mình làm cho
Bài 5 :
b, A = x(2x-3)
A= 2x2-3x
A= 2(x2-3/2x)
A= 2(x2-2x3/4+9/16-9/16)
A=2[(x-3/4)2-9/16]
A=2(x-3/4)2-9/8
A=2(x-3/4)2+(-9/8)
Vì (x-3/4)2 \(\ge\)0 \(\forall x\)
-> 2(x-3/4)2 \(\ge0\forall x\)
-> 2(x-3/4)2+(-9/8)\(\ge-\frac{9}{8}\forall x\)
Vậy MinA= -9/8
Bài 1:
1. Khai triển hằng đẳng thức
(x+3)2 = x2+6x+9
2. Thực hiện phép tính
a) 2x2(3x-5x3)+10x5-5x3
=6x3-10x5+10x5-5x3
=x3
b)(x+3)(x2-3x+9)+(x-9)(x+3)
=(x3+27)+(x2+3x-9x-27)
=x3+27+x2+3x-9x-27
=x3+x2-6x
Bài 2:
a) x2-25x=0
\(\Leftrightarrow\)x(x-25)=0
\(\Leftrightarrow\) \(\left[\begin{matrix}x=0\\x-25=0\end{matrix}\right.\)
\(\Leftrightarrow\left[\begin{matrix}x=0\\x=25\end{matrix}\right.\)
Vậy x=0 hoặc x=25
b)(4x-1)2 - 9=0
\(\Leftrightarrow\)(4x-1+3)(4x-1-3)=0
\(\Leftrightarrow\)(4x+2)(4x-4)=0
\(\Leftrightarrow\)2(2x+1)(2x-2)=0
\(\Leftrightarrow\left[\begin{matrix}2x+1=0\\2x-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left[\begin{matrix}x=\frac{-1}{2}\\x=1\end{matrix}\right.\)
Vậy x=1 hoặc x=\(\frac{-1}{2}\)
Bài 3:
a) 3x2-18x+27
=3(x2-6x+9)
=3(x-3)2
b) xy-y2-x+y
=(xy-y2)-(x-y)
=y(x-y)-(x-y)
=(x-y)(y-1)
c) x2-5x-6
=x2-6x+x-6
=(x2-6x)+(x-6)
=x(x-6)+(x-6
=(x-6)(x+1)
Bài 4:
a) (12x3y3-3x2y3+4x2y4) : 6x2y3
=x2y3(12x-3+4y): 6x2y3
=(12x-3+4y) : 6
= (12x : 6)-(3 : 6)+(4y : 6)
=2x-\(\frac{1}{2}\)+\(\frac{2y}{3}\)
b) (6x3-19x2+23x-12) : (2x-3)
=(3x2-5x+4)(2x-3) : (2x-3)
=3x2-5x+4

a) \(4x^2+4xy+y^2=\left(2x+y\right)^2\)
b) \(-x^2+2xy-y^2=-\left(x-y\right)^2\)
c) \(-4x^4-4x^2=-4x^2\left(x^2-1\right)=-4x^2\left(x-1\right)\left(x+1\right)\)
d) \(\dfrac{1}{9}x^2-\dfrac{2}{3}x+1=\left(\dfrac{1}{3}x-1\right)^2\)
e) \(\left(4x^2+1\right)^2-16x^2=\left(4x^2+1+4x^2\right)\left(4x^2+1-4x^2\right)=8x^2+1\)
f) \(16x^2-\left(x^2+4\right)^2=\left(4x^2+x^2+4\right)\left(4x^2-x^2-4\right)=\left(5x^2+4\right)\left(3x^2-4\right)\)
g) \(x^2+6x^2+12x+8=\left(x+2\right)^3\)
h) \(27x^3-54x^2+36x-8=\left(3x-2\right)^3\)
i) \(x^3-\dfrac{3}{2}x^2+\dfrac{3}{4}x-\dfrac{1}{8}=\left(x-\dfrac{1}{2}\right)^3\)
k) \(0,125x^3-0,75x^2+1,5x-1=\left(0,5-1\right)^3\)