Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/ ĐKXĐ: \(\cos2x\ne0\)
\(\frac{\cos4x}{\cos2x}=\frac{\sin2x}{\cos2x}\)\(\Leftrightarrow\cos4x-\sin2x=0\)
\(\Leftrightarrow2\cos^22x-1-\sin2x=0\)
\(\Leftrightarrow2-2\sin^22x-1-\sin2x=0\)
\(\Leftrightarrow2\sin^22x+\sin2x-1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sin2x=\frac{1}{2}=\sin\frac{\pi}{6}\\\sin2x=-1=\sin\frac{-\pi}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=\frac{\pi}{6}+2k\pi\\2x=\frac{5\pi}{6}+2k\pi\\2x=\frac{-\pi}{2}+2k\pi\left(l\right)\\2x=\frac{3\pi}{2}+2k\pi\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{12}+k\pi\\x=\frac{5\pi}{12}+k\pi\end{matrix}\right.\)
2/ \(\sin2.4x+\cos4x=1+2\sin2x.\cos\left(2x+4x\right)\)
\(\Leftrightarrow2\sin4x.\cos4x+\cos4x=1+2\sin2x.\left(\cos2x.\cos4x-\sin2x.\sin4x\right)\)
\(\Leftrightarrow2\sin4x.\cos4x+\cos4x=1+2\sin2x.\cos2x.\cos4x-2\sin^22x.\sin4x\)
\(\Leftrightarrow2\sin4x.\cos4x+\cos4x=1+\sin4x.\cos4x-\sin4x+\cos4x.\sin4x\)
Đến đây bn tự giải nốt nhé, lm kiểu bthg thôi bởi vì đã quy về hết sin4x và cos4x r

\(\Leftrightarrow\sqrt{2}sin\left(x+\frac{\pi}{4}\right)=\sqrt{2}cos3x\)
\(\Leftrightarrow cos3x=sin\left(x+\frac{\pi}{4}\right)\)
\(\Leftrightarrow cos3x=cos\left(\frac{\pi}{4}-x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=\frac{\pi}{4}-x+k2\pi\\3x=x-\frac{\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{16}+\frac{k\pi}{2}\\x=-\frac{\pi}{8}+k\pi\end{matrix}\right.\)
\(\Rightarrow x=\left\{\frac{\pi}{16};\frac{9\pi}{16};\frac{7\pi}{8}\right\}\)

Hướng dẫn giải:
Chọn A
Ta có: cos5x + cos2x + 2sin3x. sin2x =0
<=> cos 5x + cos2x - cos5x + cosx = 0
<=> cos2x + cosx = 0 <=> 2cos2x – 1 + cosx =0
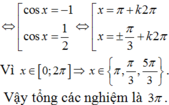


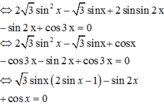
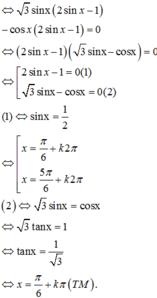
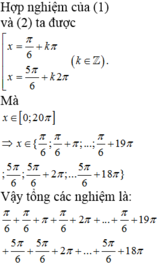
\(2sinx-\sqrt{3}=0\)
\(\Leftrightarrow sinx=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\dfrac{2\pi}{3}+k2\pi\end{matrix}\right.\)
\(0\le\dfrac{\pi}{3}+k2\pi\le2\pi\Leftrightarrow-\dfrac{1}{6}\le k\le\dfrac{5}{6}\Leftrightarrow k=0\Rightarrow x=\dfrac{\pi}{3}\)
\(0\le\dfrac{2\pi}{3}+k2\pi\le2\pi\Leftrightarrow-\dfrac{1}{3}\le k\le\dfrac{4}{6}\Leftrightarrow k=0\Rightarrow x=\dfrac{2\pi}{3}\)
\(\Rightarrow x_1+x_2=\pi\)