Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^9+2^{10}\right)\)
\(A=2.\left(1+2\right)+2^3.\left(1+2\right)+...+2^9.\left(1+2\right)\)
\(A=2.3+2^3.3+...+2^9.3\)
\(A=3.\left(2+2^3+...+2^9\right)⋮3\)
A = 2 + 22 +...+ 210 ( có 10 số hạng)
A = (2+22 ) +( 23+24) + ...+ (29+210)
A = 2.(1+2) + 23.(1+2) + ...+ 29.(1+2)
A = 2.3 + 23.3 + ...+ 29.3
A = 3.(2+23 +...+29) chia hết cho 3

Ta có 2A=22+23+...+211
=>2A-A=(22+23+...+211)-(2+22+23+...+210)
=>A=211-2=2.(210-1)
=2.1024-1=2.1023
Do 1023 chia hết cho 3=>A chia hết cho 3
A có 10 số hạng, ta chia A thành 5 nhóm, mỗi nhóm có 2 số hạng như sau:
A = 2 + 22 + 23 + 24 + 25 + 26 + 27 + 28 + 29 + 210
= (2 + 22) + (23 + 24) + (25 + 26) + (27 + 28) + (29 + 210)
= 2(1 + 2) + 23(1 + 2) + 25(1 + 2) + 27(1 + 2) + 29(1 + 2)
= 2.3 + 23.3 + 25.3 + 27.3 + 29.3
= (2 + 23 + 25 + 27 + 29).3 \(⋮\) 3
Vậy A \(⋮\) 3

=>A=2(2+1) + 2^3(2+1) + 2^5(2+1) + 2^7(2+1) + 2^9(2+1)
=>A=3(2+2^3+2^5+2^7+2^9) chia hết cho 3

\(=2\left(1+2\right)+2^3\left(1+2\right)+2^5\left(1+2\right)+2^7\left(1+2\right)+2^9\left(1+2\right)\)
\(=3\left(2+2^3+2^5+2^7+2^9\right)⋮3\)

Ta có :
\(2+2^2+2^3+....+2^{10}\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+....+2^9\left(1+2\right)\)
\(=2.3+2^3.3+....+2^9.3\)
=> Tổng chia hết cho 3
\(2+2^2+2^3+...+2^{10}\)
\(=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^9+2^{10}\right)\)
\(=2\left(1+2\right)+2^3\left(1+2\right)+...+2^9\left(1+2\right)\)
\(=2.3+2^3.3+...+2^9.3\)
\(=\left(2+2^3+...+2^9\right).3⋮3\)
\(\Rightarrow2+2^2+2^3+...+2^{10}⋮3\)
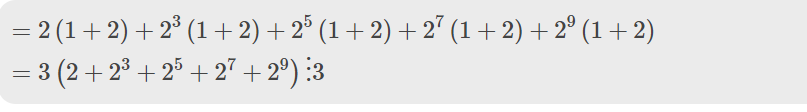
A không chia hết cho 3 vì nếu muốn 1 tổng chia hết cho 1 số thì các số hạng trong tổng đó cũng phải chia hết cho số đó
Nên 2 và 1 vài số khác cũng ko chia hết cho 3 nên tổng a ko chia hết cho 3
=> A không chia hết 3
A= (2+2^2)+...+(2^9+2^10)
A= 2.(1+2) +...+ 2^9.(1+2)
A= 2.3+...+ 2^9.3 chia hết cho 3