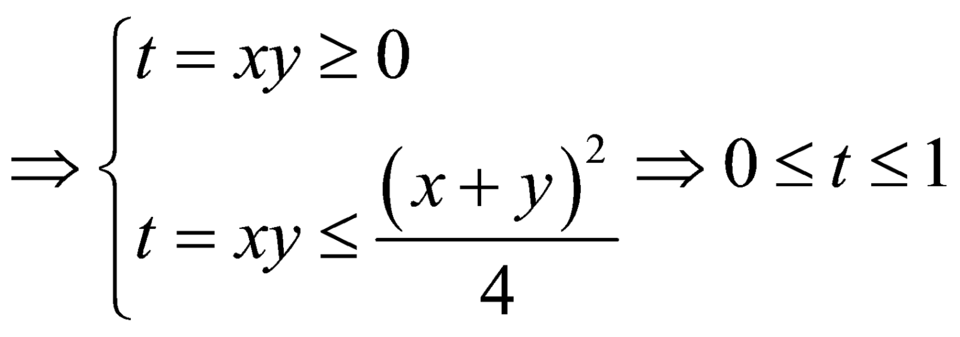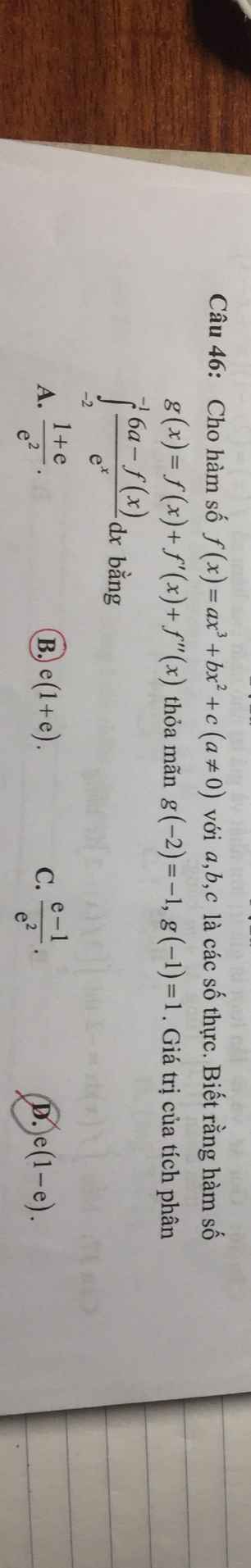Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Từ giả thiết
Trắc nghiệm rất lẹ (chắc vài giây), còn tự luận hơi lâu:
Hiển nhiên chỉ cần xét với \(x>2\) (vì vế trái luôn dương). Chú ý rằng \(a^{logx}=x^{loga}\)
Với \(a=10\Rightarrow x+2=x-2\) vô nghiệm (ktm)
- Trắc nghiệm: với \(a>10\Rightarrow\left(x^{loga}+2\right)^{loga}>x+2>x-2\) pt vô nghiệm
Với \(a< 10\) chọn 2 giá trị a=2 và a=9 để kiểm tra hàm \(\left(x^{loga}+2\right)^{loga}-x+2\) thấy đều đổi dấu ở chế độ table \(\Rightarrow a=\left\{2;3;...;9\right\}\) có 8 giá trị nguyên
- Tự luận: xét với \(x>2\), đặt \(loga=m>0\) pt trở thành: \(\left(x^m+2\right)^m=x-2\)
Đặt \(x^m+2=t\Rightarrow\left\{{}\begin{matrix}x^m=t-2\\t^m=x-2\end{matrix}\right.\)
\(\Rightarrow x^m-t^m=t-x\Rightarrow x^m+x=t^m+t\) (1)
Xét hàm \(f\left(x\right)=x^m+x\Rightarrow f'\left(x\right)=mx^{m-1}+1>0\Rightarrow f\left(x\right)\) đồng biến
Do đó \(\left(1\right)\Rightarrow x=t\Rightarrow x^m=x-2\Rightarrow x^m-x+2=0\)
Xét hàm \(f\left(x\right)=x^m-x+2\)
- Với \(m>1\Rightarrow f'\left(x\right)=m.x^{m-1}-1>1-1\ge0\Rightarrow f\left(x\right)\) đồng biến
\(\Rightarrow f\left(x\right)>f\left(2\right)=2^m-2+2=2^m>0\Rightarrow f\left(x\right)\) vô nghiệm (ktm)
- Với \(0< m< 1\) ta có:
\(f\left(2\right)=2^m>0\)
\(\lim\limits_{x\rightarrow+\infty}\left(x^m-x+2\right)=\lim\limits_{x\rightarrow+\infty}x\left(x^{m-1}-1+\dfrac{2}{x}\right)\)
Chú ý rằng \(m< 1\Rightarrow x^{m-1}=\dfrac{1}{x^{1-m}}\rightarrow0\) khi \(x\rightarrow+\infty\Rightarrow x^{m-1}-1+\dfrac{2}{x}\rightarrow-1\Rightarrow\lim\limits_{x\rightarrow+\infty}\left(x^m-x+2\right)=-\infty\)
\(\Rightarrow f\left(2\right).\lim\limits_{x\rightarrow+\infty}f\left(x\right)< 0\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thỏa mãn \(x>2\)
Vậy \(0< m< 1\) hay \(0< loga< 1\Rightarrow2\le a< 10\Rightarrow a=\left\{2;3;...;9\right\}\)
\(F\left(x\right)=\int\left(e^x.ln\left(ax\right)+\dfrac{e^x}{x}\right)dx=\int e^xln\left(ax\right)dx+\int\dfrac{e^x}{x}dx=\int e^xlnxdx+\int\dfrac{e^x}{x}dx+\int e^x.lna.dx\)
Xét \(I=\int e^xlnxdx\)
Đặt \(\left\{{}\begin{matrix}u=lnx\\dv=e^xdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=\dfrac{dx}{x}\\v=e^x\end{matrix}\right.\)
\(\Rightarrow I=lnx.e^x-\int\dfrac{e^x}{x}dx\)
\(\Rightarrow F\left(x\right)=e^x.lnx+e^x.lna+C\)
\(F\left(\dfrac{1}{a}\right)=e^{\dfrac{1}{a}}ln\left(\dfrac{1}{a}\right)+e^{\dfrac{1}{a}}.lna+C=0\Rightarrow C=0\)
\(F\left(2020\right)=e^{2020}ln\left(2020\right)+e^{2020}.lna=e^{2020}\)
\(\Rightarrow ln\left(2020a\right)=1\Rightarrow a=\dfrac{e}{2020}\)
Có bao nhiêu số nguyên y sao cho tồn tại x∈ (\(\dfrac{1}{2}\) ;8) thỏa mãn 92\(x^2\)+xy= (1+xy).915x
\(I=\int\limits^{-1}_{-2}\dfrac{6a}{e^x}dx-\int\limits^{-1}_{-2}\dfrac{f\left(x\right)}{e^x}dx=J-I_1\)
Xét \(I_1\) , đặt \(\left\{{}\begin{matrix}u=f\left(x\right)\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'\left(x\right)dx\\v=-e^{-x}\end{matrix}\right.\)
\(\Rightarrow I_1=-f\left(x\right).e^{-x}|^{-1}_{-2}+\int\limits^{-1}_{-2}\dfrac{f'\left(x\right)}{e^x}dx=-f\left(-1\right).e+f\left(-2\right).e^2+I_2\)
Xét \(I_2\) , đặt \(\left\{{}\begin{matrix}u=f'\left(x\right)\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f''\left(x\right)dx\\v=-e^{-x}\end{matrix}\right.\)
\(\Rightarrow I_2=-f'\left(x\right).e^{-x}|^{-1}_{-2}+\int\limits^{-1}_{-2}\dfrac{f''\left(x\right)}{e^x}dx=-f'\left(-1\right).e+f'\left(-2\right).e^2+I_3\)
Xét \(I_3\) , đặt \(\left\{{}\begin{matrix}u=f''\left(x\right)\\dv=e^{-x}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=f'''\left(x\right)dx=6a.dx\\v=-e^{-x}\end{matrix}\right.\)
\(\Rightarrow I_3=-f''\left(x\right).e^{-x}|^{-1}_{-2}+\int\limits^{-1}_{-2}\dfrac{6a}{e^x}dx=-f''\left(-1\right).e+f''\left(-2\right).e^2+J\)
Do đó:
\(I=J+f\left(-1\right).e-f\left(-2\right).e^2+f'\left(-1\right).e-f'\left(-2\right).e^2+f''\left(-1\right).e-f''\left(-2\right).e^2-J\)
\(=e\left[f\left(-1\right)+f'\left(-1\right)+f''\left(-1\right)\right]-e^2\left[f\left(-2\right)+f'\left(-2\right)+f''\left(-2\right)\right]\)
\(=e.g\left(-1\right)-e^2.g\left(-2\right)=e+e^2=e\left(e+1\right)\)
