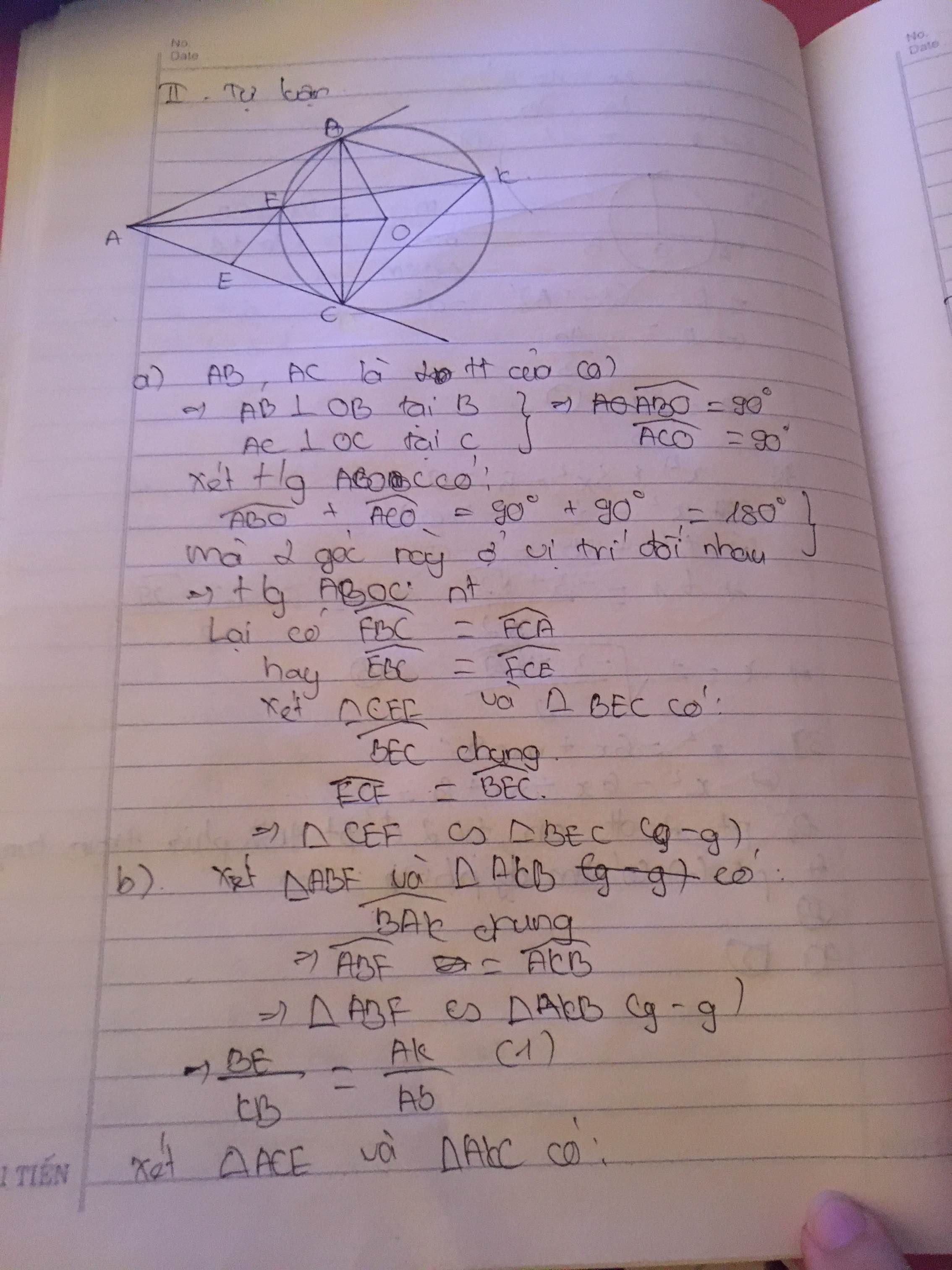Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hai tam giác được gọi là đồng dạng nếu một trong chúng bằng với một tam giác nhận được từ tam giác kia sau một phép vị tự. Các điều kiện cần và đủ để hai tam giác đồng dạng:
- Hai tam giác có các cặp cạnh tương ứng tỷ lệ thì đồng dạng.
- Hai tam giác có hai cặp góc tương ứng bằng nhau thì đồng dạng.
- Hai tam giác có hai cặp cạnh tương ứng tỷ lệ, góc xen giữa hai cặp cạnh ấy bằng nhau thì đồng dạng.

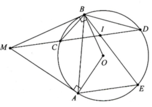
a, Vì M B C ^ = M D B ^ = 1 2 s đ C B ⏜ nên chứng minh được ∆MBC:∆MDB (g.g)
b, Vì
M
B
O
^
+
M
A
O
^
=
180
0
nên tứ giác MAOB nội tiếp
c, Đường tròn đường kính OM là đường tròn ngoại tiếp tứ giác MAOB => r = M O 2
Gọi H là giao điểm của AB với OM
=> OH ⊥ AB; AH = BH = R 3 2
Giải tam giác vuông OAM, đường cao AH ta được OM = 2R Þ r = R
d, Ta có M I B ^ = s đ D E ⏜ + s đ B C ⏜ 2 và M A B ^ = s đ A C ⏜ + s đ B C ⏜ 2
Vì AE song song CD => s đ D E ⏜ = s đ A C ⏜ => M I B ^ = M A B ^
Do tứ giác MAIB nội tiếp hay 5 điểm A, B, O, I, M nằm trên cùng 1 đường tròn kính MO
Từ đó ta có được M I O ^ = 90 0 => OI ⊥ CD hay I là trung điểm của CD

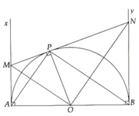
a, Sử dụng các tứ giác nội tiếp chứng minh được P M O ^ = P A O ^ và P N O ^ = P B O ^ => ∆MON và ∆APB đồng dạng (g.g)
b, Theo tính chất hai tiếp tuyến cắt nhau ta có: MP = MA và NP = NB
Mặt khác MP.NP = P O 2 và PO = R Þ AM.BN = R 2 (ĐPCM)
c, Ta có A M = R 2 => M P = R 2
Mặt khác A M = R 2 => BN = 2R => PN = 2R
Từ đó tìm được MN = 5 R 2
Vì DMON và DAPB đồng dạng nên S M O N S A P B = M N A B 2 = 25 16
d, Khi quay nửa đường tròn đường kính AB xung quanh AB ta được hình cầu với tâm O và bán kính R' = OA = R
Thể tích hình cầu đó là V = 4 3 πR 3 (đvdt)

tứ giác AECF có góc AEC=AFC là 2 góc kề nhìn cạnh AC nên nt đg tròn
b) ta có : góc ABK =0,5 sđ cung AK=90 độ
xet tam giac ABK và AFC có
góc ABK=góc AFC=90 độ
goc AKB =góc ACF (GÓC NT CHAN CUNG AB)
=>Tam giác ABK đồng dạng vs tam giác AFC(G.G)
Tứ giác AECF có góp AEC=ACF laf2 góc kề nhìn cạnh AC nên nối tiếp đường tròn
B)Ta có:Góc ABK=0,5 sđ cùng AK=90 độ
Xét tam giác ABK

a), b) HS tự chứng minh
c, AM = R 2 => S M O N S A P B = 25 16
d, V = 4 3 πR 3