Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Viết lại S như sau: S= 13+23+33+43+......+ (n-1)3+n3
Ta cần nhớ lại hằng đẳng thức bậc 3 sau:
a3+b3=(a+b)3-3ab(a+b),rồi ghép các cặp số liền kề với nhau là được VD như 1 và 2, 3 và 4, n-1 và n
Khi đó S sẽ trở thành: S=(1+2)3-3.1.2(1+2) + (3+4)3 -3.3.4(3+4) +....+ (n-1+n)^3 -3.n.(n-1)(n-1-n)
\(\Leftrightarrow\) S=(1+2)3-3.1.2(1+2) + (3+4)3 -3.3.4(3+4) +....+(2n-1)^3-3n(n-1)(2n-1)
Kết quả chung cuộc:
S= tổng xích ma k chạy từ 1 tới n của (2k-1)3 -3k(k-1)(2k-1).
Xong rồi đấy! Hoặc bạn có thể nhớ nhanh như sau: 13+23+...+n3 =(1+2+3+n)2. Vẫn giống như trên thôi.
Chúc bạn học tốt
Tham khảo :
Câu hỏi của Nguyễn Thị Ngọc Lan - Toán lớp 7 - Học toán với ...


:v cả chuyên mục câu hỏi hay :V
Câu 1:
Số số hạng của dãy là:
(99-1):1+1=99( số hạng)
Tổng của dãy trên là:
(99+1).99:2=4950
Câu 2:
Số hạng của dãy là:
(999-1):2+1=500 ( số hạng)
Tổng của dãy trên là:
(999+1).500:2=250000
Câu 3:
Số hạng của dãy là:
(998-10):2+1=495 ( số hạng)
Tổng của dãy trên là:
(998+10).495:2=249480
Bài 1
Số số hạng = ( 99 - 1 ) : 2 + 1 = 99
B = ( 1 + 99 ) x 99 : 2 = 4950
Bài 2
Số số hạng = ( 999 - 1 ) : 2 + 1 = 500
C = ( 1 + 999 ) x 500 : 2 = 250000
Bài 3
Số số hạng = ( 998 - 10 ) : 2 + 1 = 495
D = ( 10 + 998 ) x 495 : 2 = 249480

Giải:
a) \(-1313x^2y.2xy^3\)
\(=\left(-1313.2\right)\left(x^2.x\right)\left(y.y^3\right)\)
\(=-2626x^3y^4\)
Bậc của đơn thức là: \(3+4=7\)
b) \(1414x^3y.\left(-2x^3y^5\right)\)
\(=\left[1414.\left(-2\right)\right]\left(x^3.x^3\right)\left(y.y^5\right)\)
\(=-2828x^6y^6\)
Bậc của đơn thức là: \(6+6=12\).
Chúc bạn học tốt!!!
a) -x2y. 2xy3 = -2x3y4. Đơn thức có bậc là 7
b) x3y. (-2x3y5) = -2x6y6. Đơn thức có bậc là 12

Câu 7: \(\left|3x-\dfrac{12}{5}\right|+\left|x-\dfrac{4}{5}\right|=0\)
Ta có: \(\left\{{}\begin{matrix}\left|3x-\dfrac{12}{5}\right|\ge0\forall x\\\left|x-\dfrac{4}{5}\right|\ge0\forall x\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}3x-\dfrac{12}{5}=0\\x-\dfrac{4}{5}=0\end{matrix}\right.\) \(\Rightarrow x=\dfrac{4}{5}=0,8\)
Câu 8: Ta có: \(\dfrac{x}{y^2}=16\Leftrightarrow\dfrac{x}{y^2}=4^2\)
\(\Rightarrow x=4^2.y^2\) (1)
Có: \(\dfrac{x}{y}=64\Leftrightarrow\dfrac{x}{y}=4^3\)
\(\Rightarrow x=4^3y\) (2)
Từ (1) và (2)
\(\Rightarrow\left\{{}\begin{matrix}x=256\\y=16\end{matrix}\right.\)
.
Câu 1 : -1,5
Câu 2 : -14
Câu 3 : 11
Câu 4 : 74
Câu 5 : 3,5
Câu 6 : 2010
Câu 7 : 0,8
Câu 8 : 256;16
Câu 9 : 12
Câu 10: 2025

A B C D E H K M
a) Xét \(\Delta\)ADB và \(\Delta\)ADE có:
AD chung
\(\widehat{BAD}\) = \(\widehat{EAD}\) (AD là tia pg của \(\widehat{BAE}\))
AB = AE (gt)
=> \(\Delta\)ADB = \(\Delta\)ADE (c.g.c)
b) Vì \(\Delta\)ADB = \(\Delta\)ADE (câu a)
nên DB = DE (2 cạnh tương ứng); \(\widehat{ABD}\) = \(\widehat{AED}\) (2 góc tương ứng) hay \(\widehat{HBD}\) = \(\widehat{KED}\)
Xét \(\Delta\)HBD vuông tại H và \(\Delta\)KED vuông tại K có:
BD = ED (cm trên)
\(\widehat{HBD}\) = \(\widehat{KED}\) (cm trên)
=> \(\Delta\)HBD = \(\Delta\)KED (cạnh huyền - góc nhọn)
=> BH = EK (2 cạnh tương ứng)
c) Vì \(\Delta\)HBD = \(\Delta\)KED (câu b)
nên \(\widehat{BDH}\) = \(\widehat{EDK}\) (2 góc tương ứng) (1)
mà EM // DK nên \(\widehat{EDK}\) = DEM (2 góc so le trong) (2)
Từ (1) và (2) suy ra \(\widehat{DEM}\) = \(\widehat{BDH}\).



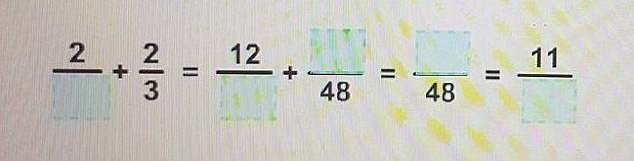

 làm giúp mik cái sáng mai nộp rui !!!,<3<3
làm giúp mik cái sáng mai nộp rui !!!,<3<3
Tính tổng $S= 1^3 + 2^3 + 3^3 +....+ n^3$ - Các dạng toán khác - Diễn đàn Toán học