K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
29 tháng 5 2020
\(\lim\limits_{x\rightarrow1}\frac{x^2+ax+b}{\left(x-1\right)\left(x+1\right)}=-\frac{1}{2}\) hữu hạn
\(\Rightarrow\) phương trình \(x^2+ax+b=0\) có 1 nghiệm bằng 1
\(\Leftrightarrow1+a+b=0\Rightarrow b=-a-1\)
\(\lim\limits_{x\rightarrow1}\frac{x^2+ax-a-1}{\left(x+1\right)\left(x-1\right)}=\lim\limits_{x\rightarrow1}\frac{\left(x+a+1\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\lim\limits_{x\rightarrow1}\frac{x+a+1}{x+1}=\frac{a+2}{2}\)
\(\Rightarrow\frac{a+2}{2}=-\frac{1}{2}\Rightarrow a=-3\Rightarrow b=2\)
\(\Rightarrow a^2+b^2=\left(-3\right)^2+2^2=13\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 6 2020
16.
\(y'=\frac{\left(cos2x\right)'}{2\sqrt{cos2x}}=\frac{-2sin2x}{2\sqrt{cos2x}}=-\frac{sin2x}{\sqrt{cos2x}}\)
17.
\(y'=4x^3-\frac{1}{x^2}-\frac{1}{2\sqrt{x}}\)
18.
\(y'=3x^2-2x\)
\(y'\left(-2\right)=16;y\left(-2\right)=-12\)
Pttt: \(y=16\left(x+2\right)-12\Leftrightarrow y=16x+20\)
19.
\(y'=-\frac{1}{x^2}=-x^{-2}\)
\(y''=2x^{-3}=\frac{2}{x^3}\)
20.
\(\left(cotx\right)'=-\frac{1}{sin^2x}\)
21.
\(y'=1+\frac{4}{x^2}=\frac{x^2+4}{x^2}\)
22.
\(lim\left(3^n\right)=+\infty\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 6 2020
11.
\(\lim\limits_{x\rightarrow1^+}\frac{-2x+1}{x-1}=\frac{-1}{0}=-\infty\)
12.
\(y=cotx\Rightarrow y'=-\frac{1}{sin^2x}\)
13.
\(y'=2020\left(x^3-2x^2\right)^{2019}.\left(x^3-2x^2\right)'=2020\left(x^3-2x^2\right)^{2019}\left(3x^2-4x\right)\)
14.
\(y'=\frac{\left(4x^2+3x+1\right)'}{2\sqrt{4x^2+3x+1}}=\frac{8x+3}{2\sqrt{4x^2+3x+1}}\)
15.
\(y'=4\left(x-5\right)^3\)
KL
7 tháng 10 2019
Tính tổng :
a) 12+322+523+....+2n−12n12+322+523+....+2n−12n
b) 12−22+32−42+....+(−1)n−1.n\(^2\)
Giải
a) HD: Đặt tổng là S\(_n\) và tính 2S\(_n\)
ĐS : S\(_n\)=3−\(\frac{2n+3}{2^n}\)
b) HD: n\(^2\)- (n+1)\(^2\)= -2n-1
Ta có: 1\(^2\)-2\(^2\)= -3; 3\(^2\) - 4\(^2\)= -7;....
Ta có: u\(_1\)= -3, d= -4 và tính S\(_n\) trong từng trường hợp n chẵn, lẻ.
Sn=3−2n+32nb) HD : b) HD : n2−(n+1)2=−2n−1n2−(n+1)2=−2n−1 Ta có 12−22=−3;32−42=−7;...12−22=−3;32−42=−7;... b) HD :
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 2 2020
\(A=lim\frac{\sqrt{n+2}+\sqrt{n+1}}{1}=lim\left[n\left(\sqrt{1+\frac{2}{n}}+\sqrt{1+\frac{1}{n}}\right)\right]=+\infty.2=+\infty\)
\(B=lim\frac{8^3.64^n-9.27^n}{4^4.64^n+5^3.25^n}=\frac{8^3-9.\left(\frac{27}{64}\right)^n}{4^4+5^3\left(\frac{25}{64}\right)^n}=\frac{8^3}{4^4}=2\)
\(1;-\frac{1}{2};\frac{1}{4}...\) là dãy cấp số nhân lùi vô hạn có \(u_1=1\) và \(q=-\frac{1}{2}\)
Do \(\left|q\right|< 1\) nên theo công thức tổng cấp số nhân:
\(S_n=\frac{u_1}{1-q}=\frac{1}{1+\frac{1}{2}}=\frac{2}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 4 2020
5.
\(\lim\limits_{x\rightarrow-\infty}\frac{-3x^5+7x^3-11}{x^5+x^4-3x}=\lim\limits_{x\rightarrow-\infty}\frac{-3+\frac{7}{x^2}-\frac{11}{x^5}}{1+\frac{1}{x}-\frac{3}{x^4}}=\frac{-3}{1}=-3\)
6.
\(\lim\limits_{x\rightarrow-4}\frac{\left(x+4\right)\left(x-1\right)}{x\left(x+4\right)}=\lim\limits_{x\rightarrow-4}\frac{x-1}{x}=\frac{-5}{-4}=\frac{5}{4}\)
7.
Khi \(x< 2\Rightarrow x-2< 0\) mà \(x+2\rightarrow4\Rightarrow\lim\limits_{x\rightarrow2^-}\frac{x+2}{x-2}=\frac{4}{-0}=-\infty\)
8.
\(\lim\limits_{x\rightarrow1}\frac{9-\left(2x+7\right)}{\left(x-1\right)\left(x+1\right)\left(3+\sqrt{2x+7}\right)}=\lim\limits_{x\rightarrow1}\frac{-2\left(x-1\right)}{\left(x-1\right)\left(x+1\right)\left(3+\sqrt{2x+7}\right)}\)
\(=\lim\limits_{x\rightarrow1}\frac{-2}{\left(x+1\right)\left(3+\sqrt{2x+7}\right)}=\frac{-2}{2.\left(3+3\right)}=-\frac{1}{6}\)
9.
\(\lim\limits_{x\rightarrow4}\frac{\left(4-x\right)\left(16-4x+x^2\right)}{4-x}=\lim\limits_{x\rightarrow4}\left(16-4x+x^2\right)=16\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 4 2020
1.
\(\lim\limits_{x\rightarrow-\infty}\frac{x^2-7x+1-\left(x^2-3x+2\right)}{\sqrt{x^2-7x+1}+\sqrt{x^2-3x+2}}=\lim\limits_{x\rightarrow-\infty}\frac{-4x-1}{\sqrt{x^2-7x+1}+\sqrt{x^2-3x+2}}\)
\(=\lim\limits_{x\rightarrow-\infty}\frac{x\left(-4-\frac{1}{x}\right)}{-x\sqrt{1-\frac{7}{x}+\frac{1}{x^2}}-x\sqrt{1-\frac{3}{x}+\frac{2}{x^2}}}=\frac{-4}{-1-1}=2\)
2.
\(\lim\limits_{x\rightarrow0^+}\frac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}=\lim\limits_{x\rightarrow0^+}\frac{\sqrt{x}+1}{\sqrt{x}-1}=-1\)
3.
\(\lim\limits_{x\rightarrow-1}\frac{x^2-3}{x^3+2}=\frac{1-3}{-1+2}=-2\) (ko phải dạng vô định, cứ thay số tính)
4.
\(\lim\limits_{x\rightarrow1}f\left(x\right)=\lim\limits_{x\rightarrow1}\frac{2x^2-x-1}{x-1}=\lim\limits_{x\rightarrow1}\frac{\left(x-1\right)\left(2x+1\right)}{x-1}=\lim\limits_{x\rightarrow1}\left(2x+1\right)=3\)
Để hs có giới hạn tại \(x=1\Rightarrow m=3\)
MC
15 tháng 3 2020
a) \(\lim\limits_{x\rightarrow0}\frac{\sqrt{1+2x}-1}{2x}=\lim\limits_{x\rightarrow0}\frac{2x}{2x\left(\sqrt{1+2x}+1\right)}=\lim\limits_{x\rightarrow0}\frac{1}{\sqrt{1+2x}+1}=\frac{1}{2}\)
b) \(\lim\limits_{x\rightarrow0}\frac{4x}{\sqrt{9+x}-3}=\lim\limits_{x\rightarrow0}\frac{4x\left(\sqrt{9+x}+3\right)}{x}=\lim\limits_{x\rightarrow0}[4\left(\sqrt{9+x}+3\right)=24\)
c) \(\lim\limits_{x\rightarrow2}\frac{\sqrt{x+7}-3}{x-2}=\lim\limits_{x\rightarrow2}\frac{x-2}{\left(x-2\right)\left(\sqrt{x+7}+3\right)}=\lim\limits_{x\rightarrow2}\frac{1}{\sqrt{x+7}+3}=\frac{1}{6}\)
d) \(\lim\limits_{x\rightarrow1}\frac{3x-2-\sqrt{4x^2-x-2}}{x^2-3x+2}=\lim\limits_{x\rightarrow1}\frac{\left(3x-2\right)^2-\left(4x^2-4x-2\right)}{(x^2-3x+2)\left(3x-2+\sqrt{4x^2-x-2}\right)}=\lim\limits_{x\rightarrow1}\frac{\left(x-1\right)\left(5x-6\right)}{\left(x-1\right)\left(x-2\right)\left(3x-2+\sqrt{4x^2-x-2}\right)}=\frac{1}{2}\\ \\\\ \\ \\ \\ \)
e)\(\lim\limits_{x\rightarrow1}\frac{\sqrt{2x+7}+x-4}{x^3-4x^2+3}=\lim\limits_{x\rightarrow1}\frac{2x+7-\left(x^2-8x+16\right)}{\left(x-1\right)\left(x^2-3x-3\right)\left(\sqrt{2x+7}-x+4\right)}=\lim\limits_{x\rightarrow1}\frac{\left(x-1\right)\left(x-9\right)}{\left(x-1\right)\left(x^2-3x-3\right)\left(\sqrt{2x+7}-x+4\right)}=\lim\limits_{x\rightarrow1}\frac{x-9}{\left(x^2-3x-3\right)\left(\sqrt{2x+7}-x+4\right)}=-8\)
f) \(\lim\limits_{x\rightarrow1}\frac{\sqrt{2x+7}-3}{2-\sqrt{x+3}}=\lim\limits_{x\rightarrow1}\frac{(2x-2)\left(2+\sqrt{x+3}\right)}{\left(1-x\right)\left(\sqrt{2x+7}+3\right)}=\lim\limits_{x\rightarrow1}\frac{-2\left(2+\sqrt{x+3}\right)}{\sqrt{2x+7}+3}=\frac{-4}{3}\)
g) \(\lim\limits_{x\rightarrow0}\frac{\sqrt{x^2+1}-1}{\sqrt{x^2+16}-4}=\lim\limits_{x\rightarrow0}\frac{x^2\left(\sqrt{x^2+16}+4\right)}{x^2\left(\sqrt{x^2+1}+1\right)}=4\)
h)
\(\lim\limits_{x\rightarrow4}\frac{\sqrt{x+5}-\sqrt{2x+1}}{x-4}=\lim\limits_{x\rightarrow4}\frac{\sqrt{x+5}-3}{x-4}+\lim\limits_{x\rightarrow4}\frac{3-\sqrt{2x+1}}{x-4}=\lim\limits_{x\rightarrow4}\frac{1}{\sqrt{x+5}+4}+\lim\limits_{x\rightarrow4}\frac{8-2x}{\left(x-4\right)\left(3+\sqrt{2x+1}\right)}=\frac{1}{7}-\frac{1}{3}=\frac{-4}{21}\)
k) \(\lim\limits_{x\rightarrow0}\frac{\sqrt{x+1}+\sqrt{x+4}-3}{x}=\lim\limits_{x\rightarrow0}\frac{\sqrt{x+1}-1}{x}+\lim\limits_{x\rightarrow0}\frac{\sqrt{x+4}-2}{x}=\lim\limits_{x\rightarrow0}\frac{1}{\sqrt{x+1}+1}+\lim\limits_{x\rightarrow0}\frac{1}{\sqrt{x+4}+2}=\frac{1}{2}+\frac{1}{4}=\frac{3}{4}\)
- Xét dãy: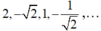
là cấp số nhân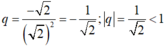 
Chọn C.