Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(I=\int\limits^{\dfrac{\pi}{4}}_0xsinxdx\)
Đặt \(\left\{{}\begin{matrix}u=x\\dv=sinxdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=dx\\v=-cosx\end{matrix}\right.\)
\(\Rightarrow I=-x.cosx|^{\dfrac{\pi}{4}}_0+\int\limits^{\dfrac{\pi}{4}}_0cosxdx=\left(-x.cosx+sinx\right)|^{\dfrac{\pi}{4}}_0=-\dfrac{\pi\sqrt{2}}{8}+\dfrac{\sqrt{2}}{2}\)

Nhân phân phối sinx vào, tách ra 2 tích phân
Tích phân đầu nguyên hàm sinx là ra
Tích phân 2, đặt t=sinx => dt=cosxdx, đổi cận, thế vào, nguyên hàm lại là ra

= -2³/3 + 2²/2 + 2.2 - [-(-1)³/3 + (-1)²/2 + 2.(-1)]
= -8/3 + 2 + 4 - 1/3 - 1/2 + 2
= 8 - 3 - 1/2
= 9/2
\(\int\limits^2_{-1}\left(-x^2+x+2\right)dx=\left(-\dfrac{x^3}{3}+\dfrac{x^2}{2}+2x\right)|^2_{-1}=\dfrac{9}{2}\)

nhaans máy tính là được mà. chuyển về chế độ radian bạn nà

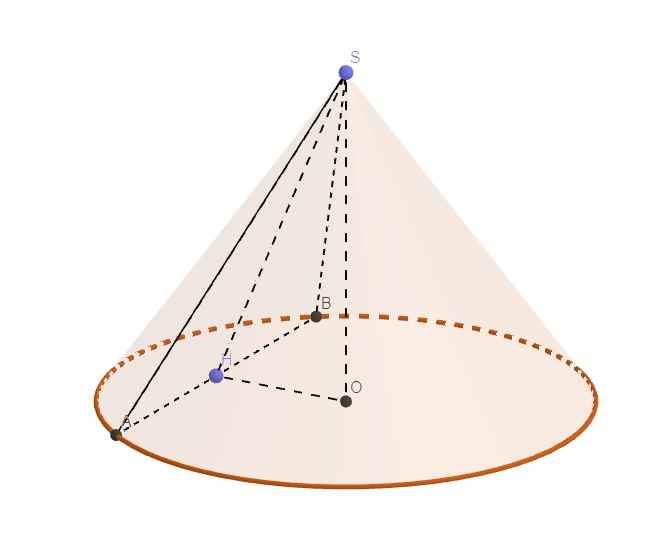
Đặt tên các điểm như hình vẽ, với H là trung điểm AB
\(\Rightarrow\widehat{SHO}=60^0\) (là góc giữa thiết diện và đáy nón)
Tam giác SAB đều \(\Rightarrow SH=\dfrac{AB\sqrt{3}}{2}=2\sqrt{3}\) (trung tuyến tam giác đều)
\(\Rightarrow\left\{{}\begin{matrix}OH=SH.cos60^0=\sqrt{3}\\h=SO=SH.sin60^0=3\end{matrix}\right.\)
\(R=OA=\sqrt{AH^2+OH^2}=\sqrt{2^2+3}=\sqrt{7}\)
\(\Rightarrow V=\dfrac{1}{3}\pi R^2h=\dfrac{1}{3}\pi.7.3=7\pi\left(cm^3\right)\)
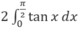
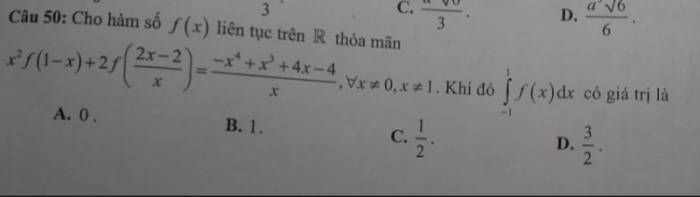 mọi người cho mình hỏi làm sao để xác định được cận của tích phân chạy từ 1 đến 2 ở bài này ?
mọi người cho mình hỏi làm sao để xác định được cận của tích phân chạy từ 1 đến 2 ở bài này ? 

Lâu ko ôn lại cũng hơi miss tích phân r :v
\(\int\limits^{\dfrac{-\pi}{4}}_{\dfrac{\pi}{4}}\tan x.dx\)
\(\int\tan x.dx=\int\dfrac{\sin x}{\cos x}.dx=-\int\dfrac{1}{\cos x}.d\left(\cos x\right)=-ln\left|\cos x\right|\)
\(\Rightarrow\int\limits^{\dfrac{-\pi}{4}}_{\dfrac{\pi}{4}}\tan x.dx=-ln\left|\cos\dfrac{-\pi}{4}\right|+ln\left|\cos\dfrac{\pi}{4}\right|\)