Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Diện tích xung quanh của hình chóp tam giác đều là:
\(\frac{{99.40}}{2}.3 = 5940\) (\(c{m^2}\))
Diện tích đáy của hình chóp là:
\(\frac{{40.34,6}}{2} = 692\) (\(c{m^2}\))
Diện tích toàn phần của hình chóp là:
\(5940 + 692 = 6632\) (\(c{m^2}\))
Thể tích của hình chóp là:
\(\frac{1}{3}.692.98,3 \approx 22674,53\) (\(c{m^3}\))
b) Diện tích xung quanh của hình chóp tứ giác đều là:
\(\frac{{91.120}}{2}.4 = 21840\) (\(c{m^2}\))
Diện tích đáy của hình chóp là:
\(120.120 = 14400\) (\(c{m^2}\))
Diện tích toàn phần của hình chóp là:
\(21840 + 14400 = 36240\) (\(c{m^2}\))
Thể tích của hình chóp là:
\(\frac{1}{3}.14400.68,4 = 328320\) (\(c{m^3}\))

a: Mặt đáy là tam giác đều cạnh 18cm
=>Chiều cao của tam giác đáy là \(18\cdot\dfrac{\sqrt{3}}{2}=9\sqrt{3}\left(cm\right)\)
b: \(V_1=\dfrac{1}{3}\cdot15\cdot\left(18^2\cdot\dfrac{\sqrt{3}}{4}\right)=5\cdot\dfrac{18^2}{4}\cdot\sqrt{3}=405\sqrt{3}\left(cm^3\right)\)
\(V_2=25\cdot30\cdot15=11250\left(cm^3\right)\)
\(\dfrac{V1}{V2}=\dfrac{405\sqrt{3}}{11250}=\dfrac{9}{250}\sqrt{3}\)

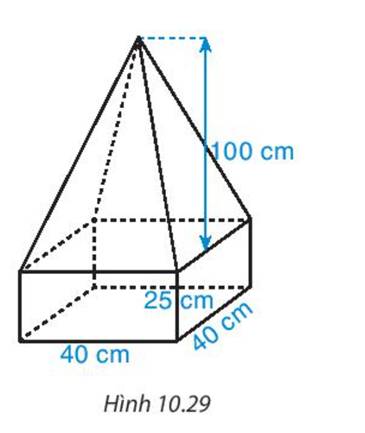
- Thể tích của hình hộp chữ nhật là: 40.40.25=40000 (cm2)
- Diện tích đáy hình chóp tứ giác đều là: 40.40=1600 (cm2)
- Thể tích hình chóp tứ giác đều là: \(V = \frac{1}{3}.S.h = \frac{1}{3}.1600.100 = \frac{{160000}}{3}\left( {c{m^3}} \right)\)
Thể tích của khối bê tông là: \(40000 + \frac{{160000}}{3} = \frac{{280000}}{3}\left( {c{m^3}} \right)\)

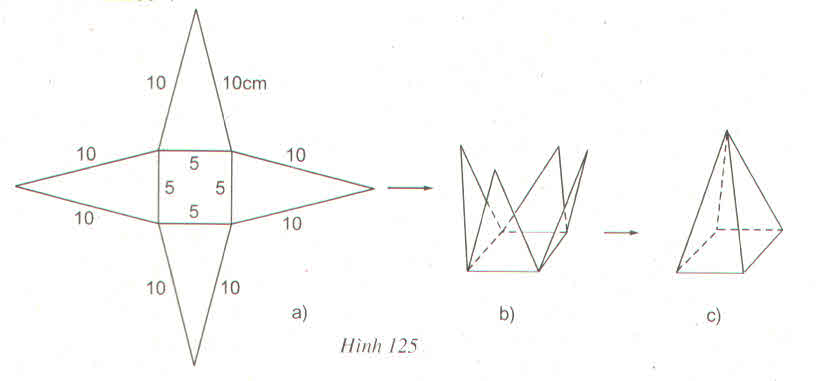
a) Trong hình 125a có 4 tam giác cân bằng nhau.
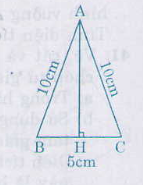
b) Chiều cao ứng với đáy của mỗi tam giác:
\(AH=\sqrt{AC^2-HC^2}\)
\(=\sqrt{AC^2-\left(\dfrac{1}{2}.5\right)^2}=\sqrt{100-\dfrac{25}{4}}=9,68\left(cm\right)\)
c) Diện tích xung quanh hình chóp:
Sxq = pd = \(\dfrac{1}{2}\).5.4.9,68 = 96,8 (cm2 )
Diện tích đáy:
Sđ = 52 = 25 (cm2 )
Diện tích toàn phần của hình chóp:
Stp = Sxq + Sđ = 121,8 (cm2 )
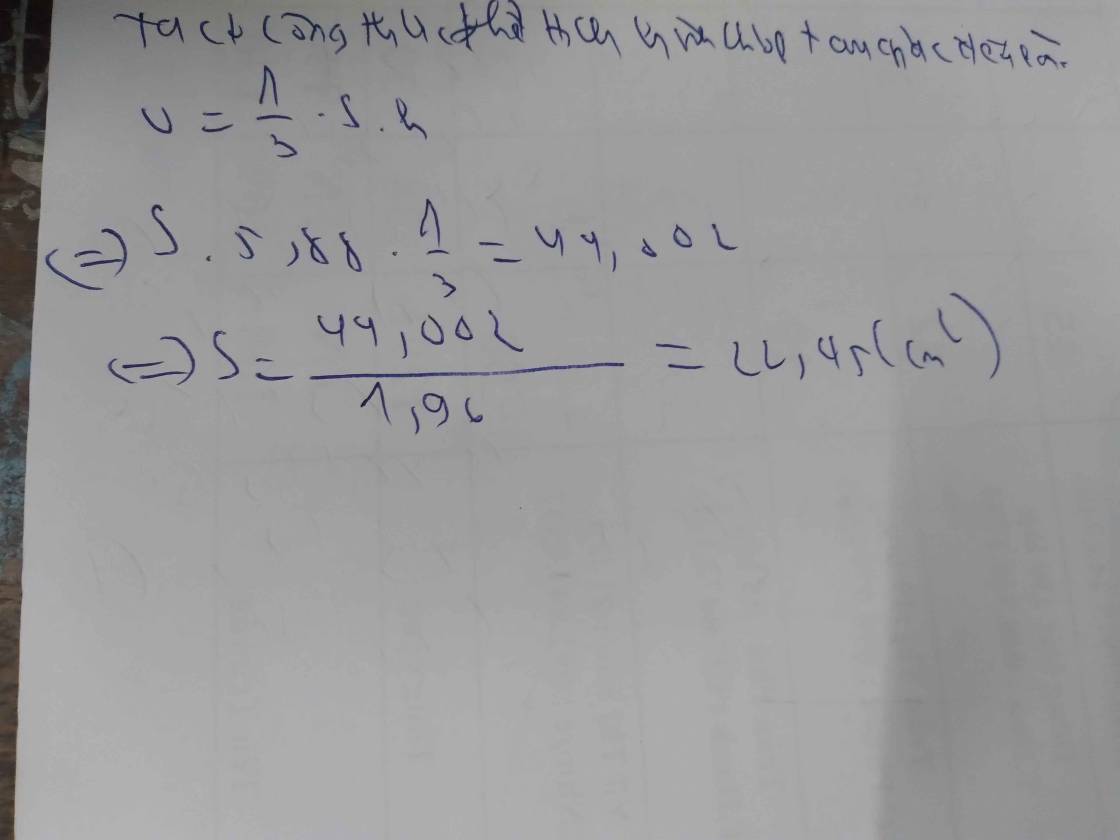



Diện tích đáy:
`(4.7 xx 4.1)/2 = 9,635 cm^2`.
Thể tích: `1/3 . 9,635 . 3,9 = 12,5255 cm^3`.