Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
đkcb: \(P_V=F_A\)
\(\Leftrightarrow0,12^3.8000=0,12^2.h_c.10000\Rightarrow h_c=0,096m\)
a: Diện tích đáy là 1280:15=256/3(cm2)
Độ dài đáy là: \(\sqrt{\dfrac{256}{3}}=\dfrac{16}{\sqrt{3}}\left(cm\right)\)
b: \(Sxq=\dfrac{1}{2}\cdot17\cdot\dfrac{16}{\sqrt{3}}\cdot4\simeq78,52\left(cm^2\right)\)
( Vào TKHĐ là thấy hính nha bạn )
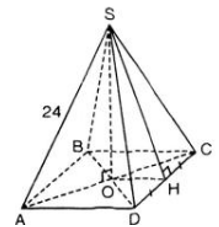
a) S.ABCD là hình chóp tứ giác đều
=> ABCD là hình vuông
=> .\(AC=AB\sqrt{2}=20\sqrt{2}\left(cm\right)\)
SO là chiều cao của hình chóp
=> O = AC ∩ BD và SO ⊥ (ABCD)
=> SO ⊥ AO
=> ΔSAO vuông tại O
=> SO2 + OA2 = SA2
\(\Rightarrow SO^2=SA^2-OA^2=SA^2-\left(\frac{AC}{2}\right)^2=24^2-\left(\frac{20\sqrt{2}}{2}\right)^2=376\)
=> SO = \(\sqrt{376}\approx19,4\left(cm\right)\)(cm).
Thể tích hình chóp :
\(V=\frac{1}{3}SO.S_{ABCD}=\frac{1}{3}.\sqrt{376}.20^2=2585,43\left(cm^3\right)\)
b) Gọi H là trung điểm của CD :
\(SH^2=SD^2-DH^2=24^2-\left(\frac{20}{2}\right)^2=476\)
\(\Rightarrow SH=\sqrt{476}\approx21,8\left(cm\right)\)
=> Sxq = p.d = 2.AB.SH = \(2.20.\sqrt{476}\approx\) 872,7 (cm2 ).
Sđ = AB2 = 202 = 400 (cm2 )
⇒ Stp = Sxq + Sđ = 872,7 + 400 = 1272,7 (cm2 ).
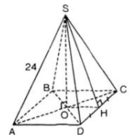
a) S.ABCD là hình chóp tứ giác đều
⇒ ABCD là hình vuông
⇒ AC = AB√2 = 20√2 (cm).
SO là chiều cao của hình chóp
⇒ O = AC ∩ BD và SO ⊥ (ABCD)
⇒ SO ⊥ AO
⇒ ΔSAO vuông tại O
⇒ SO2 + OA2 = SA2
⇒ SO2 = SA2 – OA2 = SA2 – (AC/2)2 = 242 -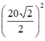 
= 376
⇒ SO = √376 ≈ 19,4 (cm).
Thể tích hình chóp:
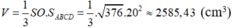
b) Gọi H là trung điểm của CD
SH2 = SD2 – DH2 = 242 –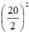 
= 476
⇒ SH = √476 ≈ 21,8 (cm)
⇒ Sxq = p.d = 2.AB.SH = 2.20.√476 ≈ 872,7 (cm2 ).
Sđ = AB2 = 202 = 400 (cm2 )
⇒ Stp = Sxq + Sđ = 872,7 + 400 = 1272,7 (cm2 ).
Bạn cần bổ sung hình để mn rõ đề của bạn hơn nhé.