Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mk pit làm phần a thui
vì AG=2GM
+) AG=4 cm
=>4=2GM
=> MG=4:2=2 (cm)
+)gm+ag=am
+)mg=2 cm
+) ag=9cm
=>2+9=am
=> am=11 cm
tính độ dài đoạn cp và bn tương tự như trên

k cho mình nhe
xét hai tam giác DGB=GEC(c.g.c)
=>BD=EC
mà BD=1/2AB
EC=1/2AC
=>AB=AC
tự Cm tiếp nhe

Xét \(\Delta ABC:\)
3 đường trung tuyến giao nhau tại G.
=> GA= 2/3 AD\(\left(Khoảngcáchgiữatrọngtâmđếncácđỉnhcủa\Delta\right)\)
GB= 2/3 BE\(\left(Khoảngcáchgiữatrọngtâmđếncácđỉnhcủa\Delta\right)\)
GC= 2/3 CF \(\left(Khoảngcáchgiữatrọngtâmđếncácđỉnhcủa\Delta\right)\)

vì G là trọng tâm của tam giác ABC ta có :
AG=2/3 AN
BG=2/3 BQ (1)
CG=2/3 CM (2)
mà 2 tam giác ACM=ABQ ( g-c-g)
suy ra CM=BQ (cạnh tương ứng) (3)
từ (2) và (3) suy ra BG=CG
>>>>>>.........''tớ chỉ pk lmf tới đây thui''.........<<<<<<<<<<


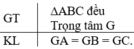
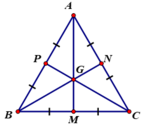
Gọi trung điểm BC, CA, AB lần lượt là M, N, P.
Khi đó AM, BN, CP đồng quy tại trọng tâm G.
Ta có: ∆ABC đều suy ra:
+ ∆ABC cân tại A ⇒ BN = CP (theo chứng minh bài 26).
+ ∆ABC cân tại B ⇒ AM = CP (theo chứng minh bài 26).
⇒ AM = BN = CP (1)
Vì G là trọng tâm của ∆ABC nên theo tính chất đường trung tuyến:
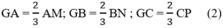
Từ (1) , (2) ⇒ GA = GB = GC.

BC = \(\sqrt{8^2+6^2}\)= 10 cm
trung truyến AM = BC/2 = 5cm
AG = 2AM/3 = 10/3 cm.
trung tuyến BN = \(\sqrt{\frac{2BC^2+2BA^2-AC^2}{4}}\)= \(\sqrt{\frac{2\left(10^2+6^2\right)-8^2}{4}}\)
BG = 2BN/3
trung tuyến CP = \(\sqrt{\frac{2BC^2+2AC^2-AB^2}{4}}\)= \(\sqrt{\frac{2\left(10^2+8^2\right)-6^2}{4}}\)
BG = 2CP/3

a) Ta có: \(\widehat{B}=2\cdot\widehat{A}\)(gt)
hay \(\widehat{B}=2\cdot50^0=100^0\)
Xét ΔABC có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)(Định lí tổng ba góc trong một tam giác)
\(\Leftrightarrow\widehat{C}=180^0-\widehat{A}-\widehat{B}\)
\(\Leftrightarrow\widehat{C}=180^0-50^0-100^0\)
hay \(\widehat{C}=30^0\)
Vậy: \(\widehat{A}=50^0\); \(\widehat{B}=100^0\); \(\widehat{C}=30^0\)
b) Ta có: \(\widehat{A}+\widehat{B}=80^0\)
\(\Leftrightarrow\widehat{A}=80^0-\widehat{B}\)
Ta có: \(\widehat{A}-\widehat{B}=40^0\)
\(\Leftrightarrow80^0-\widehat{B}-\widehat{B}=40^0\)
\(\Leftrightarrow80^0-2\cdot\widehat{B}=40^0\)
\(\Leftrightarrow2\cdot\widehat{B}=40^0\)
hay \(\widehat{B}=20^0\)
Ta có: \(\widehat{A}=80^0-\widehat{B}\)
\(\Leftrightarrow\widehat{A}=80^0-20^0\)
hay \(\widehat{A}=60^0\)
Xét ΔABC có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)(Định lí tổng ba góc trong một tam giác)
\(\Leftrightarrow\widehat{C}=180^0-\widehat{A}-\widehat{B}\)
\(\Leftrightarrow\widehat{C}=180^0-60^0-20^0\)
hay \(\widehat{C}=100^0\)
Vậy: \(\widehat{A}=60^0\); \(\widehat{B}=20^0\); \(\widehat{C}=100^0\)
c) Xét ΔABC có \(\widehat{B}=\widehat{C}\)(gt)
nên ΔABC cân tại A(Định lí đảo của tam giác cân)
Xét ΔABC cân tại A có \(\widehat{A}=60^0\)(gt)
nên ΔABC đều(Dấu hiệu nhận biết tam giác đều)
\(\Leftrightarrow\widehat{A}=\widehat{B}=\widehat{C}=60^0\)(Số đo của các góc trong ΔABC đều)
Vậy: \(\widehat{A}=60^0\); \(\widehat{B}=60^0\); \(\widehat{C}=60^0\)
d) Xét ΔABC có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)(Định lí tổng các góc trong một tam giác)
\(\Leftrightarrow\widehat{B}+\widehat{C}=180^0-\widehat{A}=180^0-60^0=120^0\)
\(\Leftrightarrow\widehat{B}=120^0-\widehat{C}\)
Ta có: \(\widehat{B}-\widehat{C}=20^0\)
\(\Leftrightarrow120^0-\widehat{C}-\widehat{C}=20^0\)
\(\Leftrightarrow120^0-2\cdot\widehat{C}=20^0\)
\(\Leftrightarrow2\cdot\widehat{C}=100^0\)
hay \(\widehat{C}=50^0\)
Ta có: \(\widehat{B}-\widehat{C}=20^0\)
\(\Leftrightarrow\widehat{B}=20^0+\widehat{C}=20^0+50^0\)
hay \(\widehat{B}=70^0\)
Vậy: \(\widehat{A}=60^0\); \(\widehat{C}=50^0\); \(\widehat{B}=70^0\)
Cám ơn bạn nhiều ạ