Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{3+5+7}=\dfrac{180^0}{15}=12^0\\ \Rightarrow\left\{{}\begin{matrix}\widehat{A}=36^0\\\widehat{B}=60^0\\\widehat{C}=84^0\end{matrix}\right.\)

Theo đề bài ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) và \(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\dfrac{\widehat{A}}{3}=\dfrac{\widehat{B}}{5}=\dfrac{\widehat{C}}{7}=\dfrac{\widehat{A}+\widehat{B}+\widehat{C}}{3+5+7}=\dfrac{180^o}{15}=12^o\)
\(\Rightarrow\widehat{A}=12^o.3=36^o\)
\(\widehat{B}=12^o.5=60^o\)
\(\widehat{C}=12^o.7=84^o\)
nếu số đo (độ) các góc của tam giác ABC là A , B , C (độ) thì theo điều kiện bài ra và tính chất của dãy tỉ số bằng nhau , ta có \(\dfrac{A}{3}=\dfrac{B}{5}=\dfrac{C}{7}=\dfrac{A+B+C}{3+5+7}=\dfrac{180}{15}=12\)
vậy : A = 3 . 12 = 36
B = 5 . 12 = 60
C = 7 . 12 = 84
=> A = 36 (độ) ; B = 60 (độ) ; C = 84 (độ)

Gọi a, b, c (độ) lần lượt là số đo 3 góc A, B, C. (0 < a; b; c < 180º).
Theo định lí tổng ba góc của tam giác ta có:
a + b + c = 180.
Vì số đo 3 góc tỉ lệ với 3; 5; 7 nên ta có:
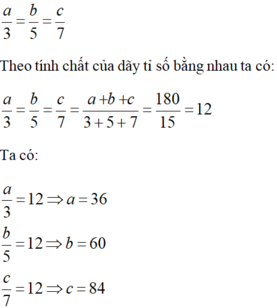
Vậy số đo ba góc của tam giác ABC là: 36o; 60o; 84o

gọi số đo 3 góc của tam giác lần lượt là a,b,c => a+b+c = 180 độ( định lí tổng 3 góc trong tam giác
tỉ lệ với 2;3;5
=> \(\frac{a}{2}=\frac{b}{3}=\frac{c}{5}\)
= \(\frac{a+b+c}{2+3+5}\) (tính chất dãy tỉ số bằng nhau)
= \(\frac{180}{10}\)(do a+b+c=180 độ)
= 18 độ
=> a = 18.2=36 độ
b = 18.3= 54 độ
c = 18.5 = 90 độ

Trong tam giác ABC có: \(\widehat A + \widehat B + \widehat C = 180^\circ \)
Mà số đo ba góc \(\widehat A,\widehat B,\widehat C\) của tam giác ABC tỉ lệ với 5;6;7 nên \(\dfrac{{\widehat A}}{5} = \dfrac{{\widehat B}}{6} = \dfrac{{\widehat C}}{7}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\begin{array}{l}\dfrac{{\widehat A}}{5} = \dfrac{{\widehat B}}{6} = \dfrac{{\widehat C}}{7} = \dfrac{{\widehat A + \widehat B + \widehat C}}{{5 + 6 + 7}} = \dfrac{{180^\circ }}{{18}} = 10^\circ \\ \Rightarrow \widehat A = 10^\circ .5 = 50^\circ \\\widehat B = 10^\circ .6 = 60^\circ \\\widehat C = 10^\circ .7 = 70^\circ \end{array}\)
Vậy số đo 3 góc \(\widehat A,\widehat B,\widehat C\) lần lượt là \(50^\circ ;60^\circ ;70^\circ \)

`a,` Gọi số đo `3` góc của Tam giác `ABC` lần lượt là `x,y,z (x,y,z \ne 0)`
Tỉ lệ thức biểu diễn mối quan hệ giữa số đo `3` góc trong Tam giác `ABC` là `x/2=y/3=z/4`
`b,` Tổng số đo `3` góc trong `1` tam giác là `180^0`
`-> x+y+z=180`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/2=y/3=z/4=(x+y+z)/(2+3+4)=180/9=20`
`-> x/2=y/3=z/4=20`
`->x=20*2=40, y=20*3=60, z=20*4=80`
Vậy, số đo của `3` góc trong Tam giác `ABC` lần lượt là `40^0, 60^0, 80^0.`
a:
Đặt \(a=\widehat{A};b=\widehat{B};c=\widehat{C}\)
a/2=b/3=c/4
b: a/2=b/3=c/4=(a+b+c)/(2+3+4)=180/9=20
=>a=40; b=60; c=80
Theo đề bài ta có: ˆA+ˆB+ˆC=180oA^+B^+C^=180o và ˆA3=ˆB5=ˆC7A^3=B^5=C^7
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
ˆA3=ˆB5=ˆC7=ˆA+ˆB+ˆC3+5+7=180o15=12oA^3=B^5=C^7=A^+B^+C^3+5+7=180o15=12o
⇒ˆA=12o.3=36o⇒A^=12o.3=36o
ˆB=12o.5=60oB^=12o.5=60o
ˆC=12o.7=84o
HT
Theo đề bài ta có: ˆA+ˆB+ˆC=180oA^+B^+C^=180o và ˆA3=ˆB5=ˆC7A^3=B^5=C^7
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
ˆA3=ˆB5=ˆC7=ˆA+ˆB+ˆC3+5+7=180o15=12oA^3=B^5=C^7=A^+B^+C^3+5+7=180o15=12o
⇒ˆA=12o.3=36o⇒A^=12o.3=36o
ˆB=12o.5=60oB^=12o.5=60o
ˆC=12o.7=84o