Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right).......\left(1-\dfrac{1}{10}\right)\)
\(=\left(\dfrac{2}{2}-\dfrac{1}{2}\right)\left(\dfrac{3}{3}-\dfrac{1}{3}\right).........\left(\dfrac{10}{10}-\dfrac{1}{10}\right)\)
\(=\dfrac{1}{2}.\dfrac{2}{3}......\dfrac{9}{10}\)
\(=\dfrac{1}{10}\)

\(\left(1-\dfrac{1}{3}\right).\left(1-\dfrac{1}{6}\right).\left(1-\dfrac{1}{10}\right).\left(1-\dfrac{1}{15}\right)...\left(1-\dfrac{1}{780}\right)\)
\(=\dfrac{2}{3}.\dfrac{5}{6}.\dfrac{9}{10}...\dfrac{779}{780}\)
\(=\dfrac{4}{6}.\dfrac{10}{12}.\dfrac{18}{20}...\dfrac{1558}{1560}\)
\(=\dfrac{4.10.18...1558}{6.12.20...1560}\)
\(=\dfrac{41}{39}.3\)
\(=\dfrac{41}{11}\)

\(T=\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{5}\right)\left(1-\dfrac{1}{7}\right)\left(1-\dfrac{1}{9}\right)\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{4}\right)\left(1-\dfrac{1}{6}\right)\left(1-\dfrac{1}{8}\right)\left(1-\dfrac{1}{10}\right)\)\(\Rightarrow T=\dfrac{2}{3}.\dfrac{4}{5}.\dfrac{6}{7}.\dfrac{8}{9}.\dfrac{10}{11}.\dfrac{1}{2}.\dfrac{3}{4}.\dfrac{5}{6}.\dfrac{7}{8}.\dfrac{9}{10}\)
\(\Rightarrow=\dfrac{1}{11}\)
\(\Rightarrow\) Số nghịch đảo của T là \(11\)

Ta có: \(A=\left(\dfrac{1}{3}-1\right)\left(\dfrac{1}{6}-1\right)\left(\dfrac{1}{10}-1\right)\left(\dfrac{1}{15}-1\right)\left(\dfrac{1}{21}-1\right)\left(\dfrac{1}{28}-1\right)\left(\dfrac{1}{36}-1\right)\)
\(=\dfrac{-2}{3}.\dfrac{-5}{6}.\dfrac{-9}{10}.\dfrac{-14}{15}.\dfrac{-20}{21}.\dfrac{-27}{28}.\dfrac{-35}{36}\)
\(=\dfrac{-2.\left(-5\right).3.\left(-3\right).2.\left(-7\right).\left(-4\right).5.\left(-3\right).9.5.\left(-7\right)}{3.2.3.2.5.3.5.3.7.4.7.4.9}\)
\(=\dfrac{-5}{3.4}=\dfrac{-5}{12}\)
Vậy \(A=\dfrac{-5}{12}.\)
\(C=1+\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2016}}\)
\(2C=2\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2016}}\right)\)
\(2C=2+1+\dfrac{1}{2}+\dfrac{1}{2^2}+....+\dfrac{1}{2^{2015}}\)
\(2C-C=\left(2+1+\dfrac{1}{2}+...+\dfrac{1}{2^{2015}}\right)-\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2016}}\right)\)
\(C=2-\dfrac{1}{2^{2016}}\)

a: \(\left(\dfrac{4}{9}+\dfrac{1}{3}\right)^2=\dfrac{49}{81}\)
b: \(\left(\dfrac{1}{2}-\dfrac{3}{5}\right)^3=-\dfrac{1}{1000}\)
c: \(\left(-\dfrac{10}{3}\right)^5\cdot\left(-\dfrac{6}{4}\right)^4=-\dfrac{6250}{3}\)
d: \(\left(\dfrac{3}{4}\right)^3:\left(\dfrac{3}{4}\right)^2:\left(-\dfrac{3}{2}\right)^3=-\dfrac{2}{9}\)
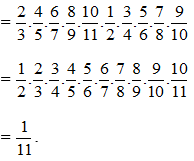
\(B=\left(\dfrac{1}{3}-1\right)+\left(\dfrac{1}{6}-1\right)+\left(\dfrac{1}{10}-1\right)+...+\left(\dfrac{1}{45}-1\right)\)
Quy luật dãy số \(B=\left(\dfrac{1}{1+2}-1\right)+\left(\dfrac{1}{1+2+3}-1\right)+\left(\dfrac{1}{1+2+3+4}-1\right)+...+\left(\dfrac{1}{1+2+..+9}-1\right)\)\(B=\left(\dfrac{1}{1+2}\right)+\left(\dfrac{1}{1+2+3}\right)+\left(\dfrac{1}{1+2+3+4}\right)+...+\left(\dfrac{1}{1+2+..+9}\right)-8\)\(B=B_1-8\)
\(\dfrac{B_1}{2}=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+..+\dfrac{1}{9}-\dfrac{1}{10}=\dfrac{1}{2}-\dfrac{1}{10}\)
\(B_1=1-\dfrac{1}{5}\)
\(B=1-\dfrac{1}{5}-8=-8-\dfrac{1}{5}=-\dfrac{41}{5}\)