Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 7:
Gọi số bị chia và số chia lần lượt là $a$ và $b$. Theo bài ra ta có:
$a+b=275$
$a=8b+5$
$\Rightarrow 8b+5+b=275$
$9b+5=275$
$9b=270$
$b=30$
Vậy số chia là $30$

a) \(1+2+3+...+48=\dfrac{\left(48+1\right)\left(\dfrac{48-1}{1}+1\right)}{2}=1176\)
b) \(2+4+6+...+212=\dfrac{\left(212+2\right)\left(\dfrac{212-2}{2}+1\right)}{2}=11342\)

a) 5.11.18 + 9.31.10 + 4.29.45
= 5.11.9.2 + 9.31.5.2 + 2.2.29.9.5
= 9.5.2.(11 + 31 + 2.29)
= 90.100
= 9000
b) 37.39 + 78.14 + 13.85 + 52.55
= 37.39 + 39.2.14 + 13.17.5 + 13.4.11.5
= 39.(37 + 2.14) + 13.5.(17 + 4.11)
= 39.65 + 65.61
= 65.(39 + 61)
= 65.100
= 6500
a) Ta có: \(5\cdot11\cdot18+9\cdot31\cdot10+4\cdot29\cdot45\)
\(=5\cdot9\left(11\cdot2+31\cdot10+4\cdot29\cdot5\right)\)
\(=5\cdot9\cdot\left(22+310+580\right)\)
\(=45\cdot912=41040\)
b) Ta có: \(37\cdot39+78\cdot14+13\cdot85+52\cdot55\)
\(=39\left(37+2\cdot14\right)+13\cdot\left(85+4\cdot55\right)\)
\(=13\left(3\cdot65+85+4\cdot55\right)\)
\(=13\cdot500=6500\)

1 + ( 2 - 3 - 4 + 5 ) + (6 - 7 - 8 + 9 ) +....+ ( 98 - 99 -100 ) 1 + 0 + 0 +...+ (-101) 1 + (-101) = 100 đúng 100 phần trăm luôn
tính tổng
1 + 2 - 3 + 4 ... + 97 + 98 - 99 - 100
nhanh lên nhé, mik cần gấp. ah mà các bn giải cụ thể giùm mik nha

\(f,=\left(5^2+3\right):7=28:7=4\\ g,=7^2-9+8\cdot25=49-9+200=240\\ h,=600+72+18=690\\ i,=5^2+5-20=10\\ j,=45-28+83=100\)

\(2A=\frac{4}{1.5}+\frac{6}{5.11}+\frac{8}{11.19}+\frac{10}{19.29}+\frac{12}{29.41}\)
\(=1-\frac{1}{5}+\frac{1}{5}-\frac{1}{11}+\frac{1}{11}-\frac{1}{19}+...+\frac{1}{29}-\frac{1}{41}=1-\frac{1}{41}=\frac{40}{41}\)
\(\Rightarrow A=\frac{20}{21}\)
\(3B=\frac{3}{1.4}+\frac{6}{4.10}+\frac{9}{10.19}+\frac{12}{19.31}=1-\frac{1}{4}+\frac{1}{4}-\frac{1}{10}+\frac{1}{10}-\frac{1}{19}+\frac{1}{19}-\frac{1}{31}\)
\(=1-\frac{1}{31}=\frac{30}{31}\)
\(\Rightarrow B=\frac{10}{31}=\frac{20}{62}<\frac{20}{41}\)
Do đó $A>B$
Ta có: \(A=\dfrac{2}{1.5}+\dfrac{3}{5.11}+\dfrac{4}{11.19}+\dfrac{5}{19.29}+\dfrac{6}{29.41}\)
\(2A=1-\dfrac{1}{5}+\dfrac{1}{5}+...+\dfrac{1}{29}-\dfrac{1}{41}\)
\(2A=1-\dfrac{1}{41}=\dfrac{40}{41}\)
\(A=\dfrac{20}{41}\)
Lại có: \(B=\dfrac{1}{1.4}+\dfrac{2}{4.10}+\dfrac{3}{10.19}+\dfrac{4}{19.31}\)
\(3B=\dfrac{3}{1.4}+\dfrac{6}{4.10}+\dfrac{9}{10.19}+\dfrac{12}{19.31}\)
\(3B=1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{10}+...+\dfrac{1}{19}-\dfrac{1}{31}\)
\(3B=1-\dfrac{1}{31}=\dfrac{30}{31}\)
\(B=\dfrac{10}{31}\)
Vì \(\dfrac{20}{41}>\dfrac{10}{31}\) nên...

gọi d là ƯCLN(18n+3,21n+7)
ta có 18n+3chia hết cho d
21n+7 chia hết cho d
⇔21n+7-18n-3 chia hết cho d
⇔126n+42-126n-21 chia hết cho d
21 chia hết cho d
⇒d∈Ư(21)=1;3;7;21
n ≠ 3k-1;3k-3;3k-7;3k-21

b: Ta có: \(\left(2+4+6+...+100\right)\cdot\left(36\cdot333-108\cdot111\right)\)
\(=\left(2+4+6+...+100\right)\cdot36\cdot111\cdot\left(3-3\right)\)
=0


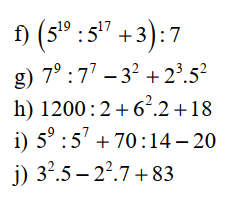 giúp mik với, mik đang cần gấp, các bạn làm nhanh giúp mik nhé, bạn nào nhanh nhất mik tặng tim
giúp mik với, mik đang cần gấp, các bạn làm nhanh giúp mik nhé, bạn nào nhanh nhất mik tặng tim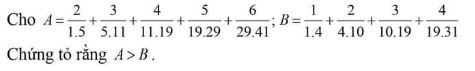


XIN LỖI CÁC BN NHÉ LÀ 37.39+14.79+13.85+52.55
\(37\cdot39+14\cdot79+13\cdot85\)
\(=13\left(37\cdot3+85\right)+14\cdot79\)
\(=13\cdot196+14\cdot79\)
\(=14\left(13\cdot14+79\right)\)
\(=14\cdot261=3654\)