Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A= 1/3 + 1/3^2 + ... + 1/3^8
3A= 3. (1/3+ 1/3^2+ ... + 1/3^8)
3A=1+ 1/3 + 1/3^2+ ... +1/3^7
=> 3A - A= (1 + 1/3 + 1/3^2 + ... + 1/3^7) - (1/3 + 1/3^2+ ... + 1/3^8)
=> 2A= 1 - 1/ 3^8
2A= 6560/6561
A= 6560/6561 : 2
A= 3280/6561

`1/5 . 4/7 + 3/7 . 1/5 -1/5`
`=1/5 . 4/7 + 3/7 . 1/5 -1/5 . 1`
`=1/5 . ( 4/7+3/7-1)`
`=1/5 . ( 7/7-1)`
`= 1/5 . 0`
`=0`
\(\dfrac{1}{5}\times\dfrac{4}{7}+\dfrac{3}{7}\times\dfrac{1}{5}-\dfrac{1}{5}=\dfrac{1}{5}\times\left(\dfrac{4}{7}+\dfrac{3}{7}-1\right)=\dfrac{1}{5}\times0=0\)

1/2^2 + 1/3^2 +... + 1/100^2 < 1/4 + 1/2.3 + 1/3.4 +... + 1/99.100
1/2^2 + 1/3^2 +... + 1/100^2 < 1/4 + 1/2 - 1/3 + 1/3 -1/4 +... + 1/99 + 1/100
1/2^2 + 1/3^2 +... + 1/100^2 < 1/4 + 1/2 - 1/100
1/2^2 + 1/3^2 +... + 1/100^2 < 3/4 - 1/100 < 3/4 (đpcm)

`1/15+1/35+1/63+1/99+1/143`
`=1/[3.5]+1/[5.7]+1/[7.9]+1/[9.11]+1/[11.13]`
`=1/2(2/[3.5]+2/[5.7]+2/[7.9]+2/[9.11]+2/[11.13])`
`=1/2.(1/3-1/5+1/5-1/7+...+1/11-1/13)`
`=1/2.(1/3-1/13)`
`=1/2 . 10/39`
`=5/39`

\(\dfrac{-1}{9}.\dfrac{-3}{5}+\dfrac{5}{-6}.\dfrac{-3}{5}-\dfrac{7}{2}.\dfrac{3}{5}\)
\(=\dfrac{3}{5}.\left(\dfrac{1}{9}+\dfrac{5}{6}-\dfrac{7}{2}\right)\)
\(=\dfrac{3}{5}.\left(\dfrac{2}{18}+\dfrac{15}{18}-\dfrac{63}{18}\right)\)
\(=\dfrac{3}{5}.\left(-\dfrac{23}{9}\right)\)
\(=-\dfrac{69}{45}\)

\(C=\dfrac{-5}{7}+\dfrac{-2}{7}+\dfrac{3}{4}+\dfrac{1}{4}+\dfrac{-1}{5}=-1+1-\dfrac{1}{5}=\dfrac{-1}{5}\)

Sửa đề: 2020/1+2019/2+...+1/2020
\(=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}}{\left(1+\dfrac{2019}{2}\right)+\left(1+\dfrac{2018}{3}\right)+...+\dfrac{1}{2020}+1+1}\)
\(=\dfrac{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}}{\dfrac{2021}{2}+\dfrac{2021}{3}+...+\dfrac{2021}{2020}+\dfrac{2021}{2021}}\)
=1/2021

\(\dfrac{1}{2.4}+\dfrac{1}{4.6}+...+\dfrac{1}{\left(2x-2\right).2x}=\dfrac{1}{8}\)
\(\Leftrightarrow\dfrac{2}{2.4}+\dfrac{2}{4.6}+...+\dfrac{2}{\left(2x-2\right).2x}=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{1}{2}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{4}+...+\dfrac{1}{2x-2}-\dfrac{1}{2x}=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{1}{2}-\dfrac{1}{2x}=\dfrac{1}{4}\)
\(\Leftrightarrow\dfrac{1}{2x}=\dfrac{1}{4}\)
\(\Leftrightarrow2x=4\\ \Leftrightarrow x=2\left(tm\right)\)
\(\Leftrightarrow\dfrac{1}{4}\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+.......+\dfrac{1}{\left(x-1\right)x}\right)=\dfrac{1}{8}\) ( đk x khác 0 , x khác 1)
\(\Leftrightarrow\dfrac{1}{4}\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+....+\dfrac{1}{x-1}-\dfrac{1}{x}\right)=\dfrac{1}{8}\)
\(\Leftrightarrow1-\dfrac{1}{x}=\dfrac{1}{2}\)
=> x =2 ( tm)
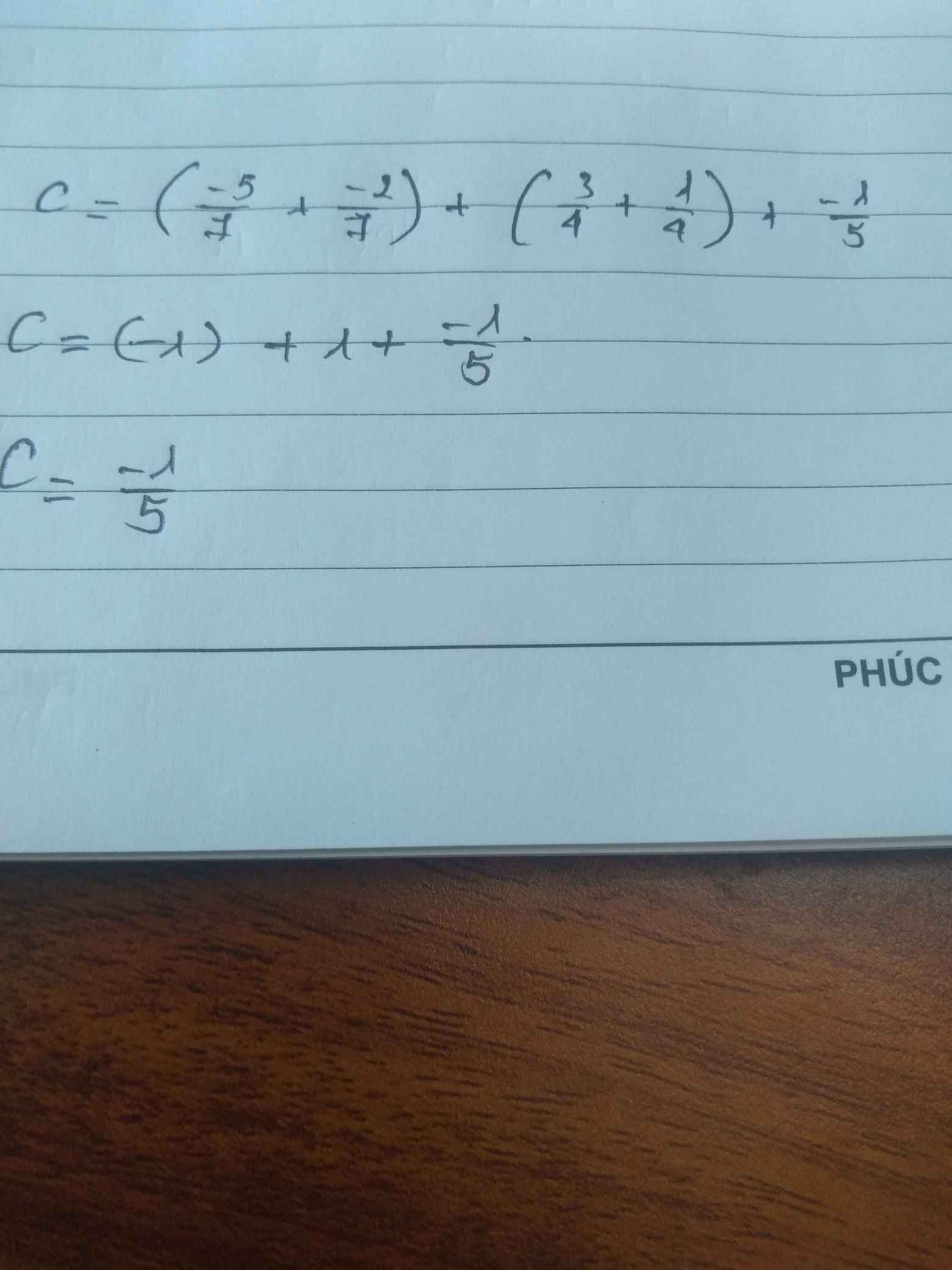
Đặt \(A=1+\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2^{2005}}\)
\(A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2005}}\)
\(2A=2\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2005}}\right)\)
\(2A=2+1+\dfrac{1}{2}+...+\dfrac{1}{2^{2004}}\)
\(2A-A=\left(2+1+\dfrac{1}{2}+...+\dfrac{1}{2^{2004}}\right)-\left(1+\dfrac{1}{2}+...+\dfrac{1}{2^{2005}}\right)\)
\(A=2-\dfrac{1}{2^{2005}}\)
Giải:
Ta có: A = \(1+\dfrac{1}{2}+\dfrac{1}{4}+...+\dfrac{1}{2^{2005}}.\)
= \(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...=\dfrac{1}{2^{2005}}.\)
2A = \(2\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2005}}\right).\)
= \(1+2+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2004}}.\)
2A -A = \(\left(1+2+\dfrac{1}{2}+...+\dfrac{1}{2^{2004}}\right)-\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2005}}\right).\)
= 2 - \(\dfrac{1}{2^{2005}}.\)
Vậy \(A=2-\dfrac{1}{2^{2005}}.\)
CHÚC BN HỌC TỐT!!! ^-^
Đừng quên bình luận nếu bài mik sai nhé!!!

