Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có: 18/27 = 2/3
theo bai ra : a/b = 18/27
=> a/b = 2/3
mà 2/3= [2.m]/[3.m]
đặt a= 2.m b=3.m
ƯCLN(a;b)=13
ƯCLN(2.m;3.m)=13
mặt khác: ƯCLN (2;3)=1
m=13
=>a/b = [2.13]/[3.13]
=26/39
đúng nhé

đề câu số 5 là chia hết cho \(5^n\)chứ ko phải là 5 đâu bạn

\(A=\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right)\left(1-\frac{1}{4}\right)...\left(1-\frac{1}{1000}\right)=\frac{1}{2}.\frac{2}{3}.\frac{3}{4}...\frac{999}{1000}=\frac{1.2.3...999}{2.3.4...1000}=\frac{1}{1000}\)
\(B=\frac{3}{4}.\frac{8}{9}.\frac{15}{16}....\frac{2499}{2500}=\frac{3.8.15...2499}{4.9.16....2500}=\frac{1.3.2.4.3.5....49.51}{2.2.3.3.4.4...50.50}=\frac{\left(1.2.3...49\right).\left(3.4.5...51\right)}{\left(2.3.4...50\right).\left(2.3.4...50\right)}\)
\(\frac{1.51}{50.2}=\frac{51}{100}\)
a. \(A=\left(1-\frac{1}{2}\right)\left(1-\frac{1}{3}\right)\left(1-\frac{1}{4}\right)....\left(1-\frac{1}{999}\right)\)
\(A=\frac{1}{2}\cdot\frac{2}{3}\cdot\frac{3}{4}\cdot....\cdot\frac{998}{999}\)
\(A=\frac{1\cdot2\cdot3\cdot....\cdot998}{2\cdot3\cdot4\cdot....\cdot999}=\frac{1}{999}\)
Vậy \(A=\frac{1}{999}\)

Ta có: 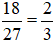
Vậy phân số tối giản của phân số
Mà ƯCLN(a ; b) = 13 nên ta có:
a : 13 = 2 ⇒ a = 26.
b : 13 = 3 ⇒ b = 39.
Vậy phân số cần tìm là
Ta có: 18/27=2/3 là phân số tối giản.
Vậy phân số tối giản của phân số a/b=2/3
Mà ƯCLN(a ; b) = 13 nên ta có: a/b=a:13/b:13=2/3
a : 13 = 2 ⇒ a = 26.
b : 13 = 3 ⇒ b = 39.
Vậy phân số cần tìm là 26/39

Ta có quy luật như sau:
S1=1.1+1^2=1
S2=2.2-1.1=2^2-1^2+4-1=3
S3=3.3-(2.2-1.1)=3^2-(2^2-1^2)=9-(4-1)=9-3=6
S4=4.4.[3.3.(2.2-1.1)]=4^2.[3^2.(2^2-1^1)]=16.[9.(4-1)]=16.(9.3)=16.27=432
S5=?
Đây là một câu hỏi dành cho những bạn chuyên toán bài trên các bạn đã được gợi ý một phần ba gợi ý rồi đấy.
S5 vẫn sẽ là một câu hỏi cho các bạn, các bạn chỉ cần tìm ra quy luật của các tổng là nhận ra ngay.
Nếu các bạn nhận ra thì chúc mừng.

2)Từ 1 đến 999 có 999 số.
Vậy tổng các chữ số của số trên :(999+1).999:2=499500
1)
Trích:
Ta có : n.n! = [(n + 1) - 1].n! = (n + 1).n! - n! = 1.2.3.....n.(n + 1) - n! = (n + 1)! - n! => |
| 1.1!+2.2!+3.3!+4.4!+5.5! =(2-1).1!+(3-1).2!+(4-1).3!+ (5-1).4!+(6-1).5! =2!-1!+3!-2!+4!-3!+5!-4!+6!-5! =6!-1!=720-1=719 |

Phân số \(\frac{a}{b}\) = \(\frac{18}{27}\) mà ƯCLN ( a, b ) = 13 là :
\(\frac{18.13}{27.13}=\frac{234}{351}\)
Vậy \(\frac{a}{b}=\frac{234}{351}\)
\(\frac{a}{b}=\frac{18}{27}=\frac{2}{3}\)
mà ƯCLN( a, b )= 13 , 13 là số nguyên tố
\(\Rightarrow a=2.13=26\)
\(b=3.13=39\)
Vậy phân số cần tìm là\(\frac{26}{39}\)
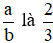
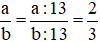
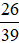
Bài 2: Ta có: \(\frac{a}{b}=\frac{18}{27}=\frac{2}{3}=\frac{2m}{3m}\)
Lại có: a=2.m
b=3.m
\(\Rightarrow\)ƯCLN\(\left(a;b\right)\)\(=m=13\)
\(\Rightarrow\frac{2m}{3m}=\frac{2.13}{3.13}=\frac{26}{39}\)