Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

N O A B
Gọi các điểm của hình sao như hình trên.
Theo đề ta có: \(AB=a\)
Mà \(AN=NB\)và \(AN+NB=AB\)
Nên \(AN=NB=\frac{AB}{2}=\frac{a}{2}\)
Ta lại có: \(NOB=\frac{1}{2}B=\frac{1}{2}.36^o=18^o\)
Xét tam giác NBO vuông tại N
\(NB=OB.\cos18^o\Rightarrow OB=\frac{NB}{\cos18^o}=\frac{a}{2\cos18^o}\)
Vậy bán kính đường tròn ngoại tiếp là \(R=\frac{a}{2\cos18^o}\)

a)
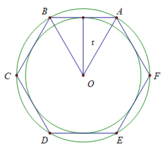
b) Cách vẽ lục giác đều có tất cả các đỉnh nằm trên đường tròn (O)
Vẽ các dây cung AB = BC = CD = DE = EF = FA = R = 2 cm
(Ta đã nêu được cách chia đường tròn thành sáu cung bằng nhau tại bài tập 10 SGK trang 71)
c) Vì các dây cung AB = BC = CD = DE = EF = FA bằng nhau nên khoảng cách từ O đến các dây là bằng nhau ( định lý liên hệ giữa dây cung và khoảng cách từ tâm đến dây)
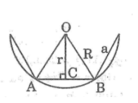

Nối các đỉnh của ngôi sao lại ta có hình ngũ giác đều nội tiếp đường tròn tâm O.
Vì là ngũ giác đều nội tiếp đường tròn tâm O nên ta có khoản cách từ O đến các đỉnh là như nhau và bằng R.
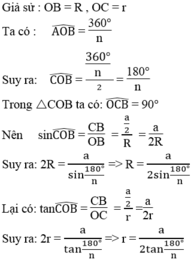
Góc tạo bởi hai đỉnh liên tiếp là
\(\frac{360}{5}=\:72°\)
Gọi khoản cách giữa 2 đỉnh liên tiếp là a thì ta có
\(a^2=R^2+R^2-2R^2\cos72°\)
Tới đây bạn tự bấm máy tính đi nhé