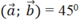Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{2.6 + ( - 3).4}}{{\sqrt {{2^2} + {{\left( { - 3} \right)}^2}} .\sqrt {{6^2} + {4^2}} }} = 0 \Rightarrow \overrightarrow a \bot \overrightarrow b \)
b) \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{3.5 + 2.( - 1)}}{{\sqrt {{3^2} + {2^2}} .\sqrt {{5^2} + {{\left( { - 1} \right)}^2}} }} = \frac{{\sqrt 2 }}{2} \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 45^\circ \)
c) \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}} = \frac{{\left( { - 2} \right).3 + ( - 2\sqrt 3 ).\sqrt 3 }}{{\sqrt {{{\left( { - 2} \right)}^2} + {{\left( { - 2\sqrt 3 } \right)}^2}} .\sqrt {{3^2} + {{\sqrt 3 }^2}} }} = - \frac{{\sqrt 3 }}{2} \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 150^\circ \)

a → . b → = a → . b → . c o s a → , b → ⇒ c o s a → , b → = a → . b → a → . b → = − 3 3.2 = − 1 2 ⇒ a → , b → = 120 0 .
Đáp án D

Ta có a → . b → = a → . b → . c o s a → , b → .
⇒ c o s a → , b → = a → . b → a → . b → = − 3 3.2 = − 1 2 ⇒ a → , b → = 120 0
Chọn D.

a → = 1 2 + 3 2 = 2 , b → = − 2 3 2 + 6 2 = 48 = 4 3
a → . b → = 1. − 2 3 + 3 .6 = 4 3
cos a → , b → = a → . b → a → b → = 4 3 2.4 3 = 1 2 ⇒ a → , b → = 60
Chọn D

Ta có: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|.\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)
\( \Leftrightarrow 12\sqrt 2 = 3.8.\cos \left( {\overrightarrow a ,\overrightarrow b } \right) \Leftrightarrow \cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\sqrt 2 }}{2}\)
\( \Rightarrow \left( {\overrightarrow a ,\overrightarrow b } \right) = 45^\circ \)
Vậy góc giữa hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) là \(45^\circ \)
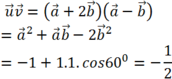
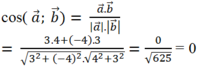
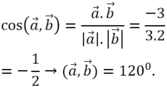
Chọn B.
Ta có:
Suy ra