
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a.\(\dfrac{2x+1}{5}-\dfrac{3+x}{10}=6\)
\(\Leftrightarrow\dfrac{2\left(2x+1\right)-\left(3+x\right)}{10}=\dfrac{60}{10}\)
\(\Leftrightarrow2\left(2x+1\right)-\left(3+x\right)=60\)
\(\Leftrightarrow4x+2-3-x=60\)
\(\Leftrightarrow3x=61\)
\(\Leftrightarrow x=\dfrac{61}{3}\)
Vậy \(S=\left\{\dfrac{61}{3}\right\}\)
b.\(\left|x-2\right|=3x+5\)
\(ĐK:x\ge-\dfrac{5}{3}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=3x+5\\2-x=3x+5\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{7}{2}\left(ktm\right)\\x=-\dfrac{3}{4}\left(tm\right)\end{matrix}\right.\)
Vậy \(S=\left\{-\dfrac{3}{4}\right\}\)



Áp dụng BĐT AM - GM ta có :
\(\left(1+\frac{a}{b}\right)^5+\left(1+\frac{b}{a}\right)^5\ge2^5\left(\sqrt{\frac{a}{b}}\right)^5+2^5\left(\sqrt{\frac{b}{a}}\right)^5=32\left[\left(\sqrt{\frac{a}{b}}\right)^5+\left(\sqrt{\frac{b}{a}}\right)^5\right]\)
\(\ge32.2\sqrt{\left(\sqrt{\frac{a}{b}}\right)^5\left(\sqrt{\frac{b}{a}}\right)^5}=32.2=64\)(đpcm)
Dấu "=" xảy ra \(\Leftrightarrow a=b\)

Áp dụng bất đẳng thức AM-GM 3 số không âm :
\(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}\ge3\sqrt[3]{\frac{abc}{abc}}=3\sqrt[3]{1}=3\)
Dấu "=" xảy ra \(\Leftrightarrow\frac{a}{b}=\frac{b}{c}=\frac{c}{a}\Leftrightarrow a=b=c\)
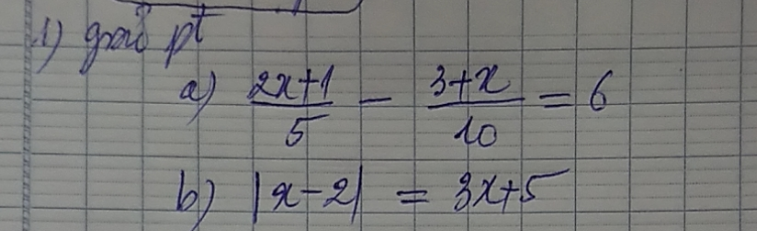 lam gium minh voi a
lam gium minh voi a