K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

MH
9 tháng 4 2017
a) Xét hiệu un+1 - un = - 2 - (
- 2) =
-
.
Vì <
nên un+1 - un =
-
< 0 với mọi n ε N* .
Vậy dãy số đã cho là dãy số giảm.
b) Xét hiệu un+1 - un =
=
Vậy un+1 > un với mọi n ε N* hay dãy số đã cho là dãy số tăng.
c) Các số hạng ban đầu vì có thừa số (-1)n, nên dãy số dãy số không tăng và cũng không giảm.
d) Làm tương tự như câu a) và b) hoặc lập tỉ số (vì un > 0 với mọi n ε N* ) rồi so sánh với 1.
Ta có
với mọi n ε N*
Vậy dãy số đã cho là dãy số giảm
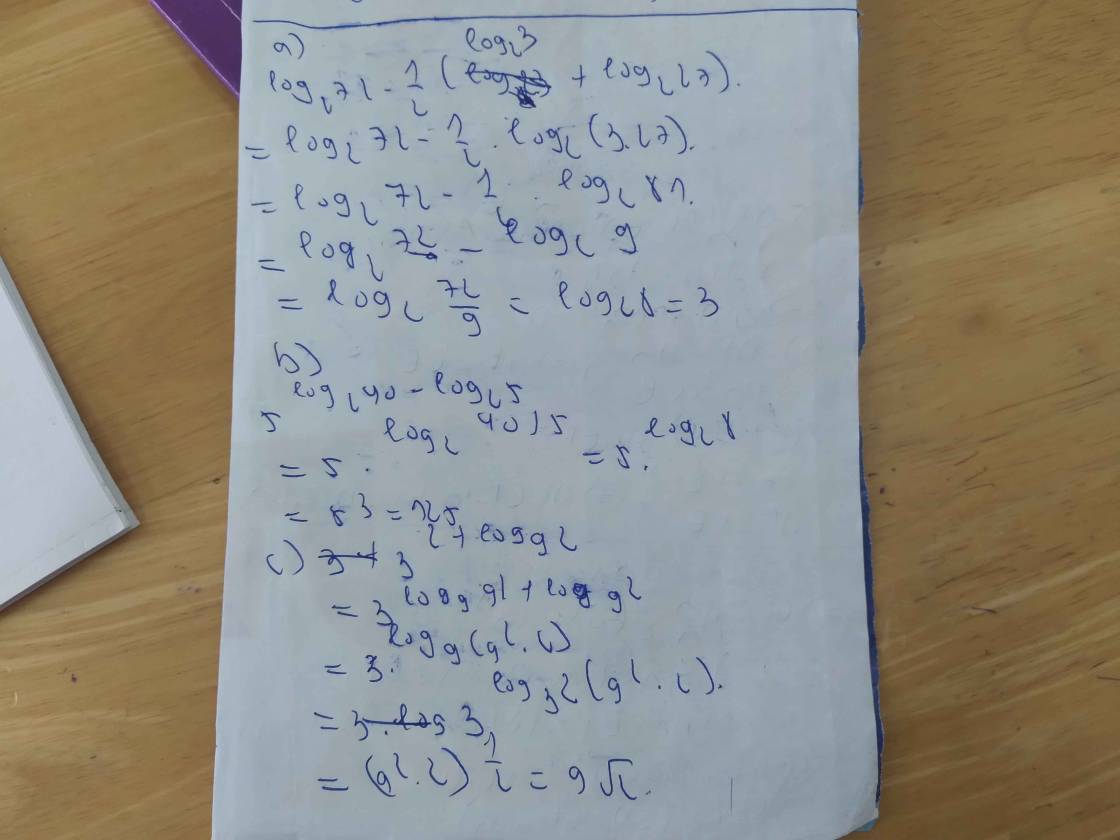




\(a,log_272-\dfrac{1}{2}\left(log_23+log_227\right)\\ =log_272-\dfrac{1}{2}log_2\left(3\cdot27\right)\\ =log_272-log_2\left(81\right)^{\dfrac{1}{2}}\\ =log_272-log_29\\ =log_2\dfrac{72}{9}\\ =log_28\\ =3\)
\(b,5^{log_240-log_25}\\ =5^{log_2\dfrac{40}{5}}\\ =5^{log_28}\\ =5^3\\ =125\)
\(c,3^{2+log_92}\\ =3^{log_9\left(81\cdot2\right)}\\ =3^{\dfrac{1}{2}log_3162}\\ =\left(162\right)^{\dfrac{1}{2}}\\ =\sqrt{162}\\ =9\sqrt{2}\)