Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=\dfrac{2^2}{1.3}+\dfrac{3^2}{2.4}+\dfrac{4^2}{3.5}+\dfrac{5^2}{4.6}+\dfrac{6^2}{5.7}\)
\(A=\dfrac{2.2.3.3.4.4.5.5.6.6}{1.3.2.4.3.5.4.6.5.7}\)
\(A=\dfrac{2.3.4.5.6}{1.2.3.4.5}.\dfrac{2.3.4.5.6}{3.4.5.6.7}\)
\(A=\dfrac{6}{1}.\dfrac{2}{7}=\dfrac{12}{7}\)
\(B=\left(1+\dfrac{1}{1.3}\right)\left(1+\dfrac{1}{2.4}\right)\left(1+\dfrac{1}{3.5}\right)\left(1+\dfrac{1}{9.11}\right)\)
\(B=\dfrac{4}{3}.\dfrac{9}{8}.\dfrac{16}{15}.\dfrac{100}{99}\)
\(B=\dfrac{4.9.16.100}{3.8.15.99}\)
\(B=\dfrac{2.2.3.3.4.4.10.10}{1.3.2.4.3.5.9.11}\)
\(B=\dfrac{2.3.4.10}{1.2.3.9}.\dfrac{2.3.4.10}{3.4.5.11}\)
\(B=10.\dfrac{2}{11}=\dfrac{20}{11}\)

\(A=-1,6:\left(1+\dfrac{2}{3}\right)\)
\(A=\dfrac{-16}{10}:\dfrac{5}{3}\)
\(A=\dfrac{-8}{5}.\dfrac{3}{5}\)
\(A=\dfrac{-24}{25}\)
\(B=1,4.\dfrac{15}{49}-\left(\dfrac{4}{5}+\dfrac{2}{3}\right):2\dfrac{1}{5}\)
\(B=\dfrac{14}{10}.\dfrac{15}{49}-\left(\dfrac{4}{5}+\dfrac{2}{3}\right):\dfrac{11}{5}\)
\(B=\dfrac{14}{10}.\dfrac{15}{49}-\dfrac{22}{15}:\dfrac{11}{5}\)
\(B=\dfrac{3}{7}-\dfrac{22}{15}:\dfrac{11}{5}\)
\(B=\dfrac{3}{7}-\dfrac{2}{3}\)
\(B=\dfrac{-5}{21}\)
\(A=-1,6:\left(1+\dfrac{2}{3}\right)\)
\(A=\dfrac{-8}{5}:\left(1+\dfrac{2}{3}\right)\)
\(A=\dfrac{-8}{5}:\dfrac{5}{3}\)
\(A=\dfrac{-24}{25}\)
\(B=1,4.\dfrac{15}{49}-\left(\dfrac{4}{5}+\dfrac{2}{3}\right):2\dfrac{1}{5}\)
\(B=\dfrac{7}{5}.\dfrac{15}{49}-\left(\dfrac{4}{5}+\dfrac{2}{3}\right):\dfrac{11}{5}\)
\(B=\dfrac{7}{5}.\dfrac{15}{49}-\dfrac{22}{15}:\dfrac{11}{5}\)
\(B=\dfrac{3}{7}-\dfrac{2}{3}\)
\(B=\dfrac{-5}{21}\)

\(B=\left(1+\dfrac{1}{8}\right)\left(1+\dfrac{1}{15}\right)\left(1+\dfrac{1}{24}\right).....\left(1+\dfrac{1}{440}\right)\left(1+\dfrac{1}{483}\right)\)
\(B=\dfrac{9}{8}.\dfrac{16}{15}.\dfrac{25}{24}.....\dfrac{441}{440}.\dfrac{484}{483}\)
\(B=\dfrac{9.16.25.....441.484}{8.15.24.....440.483}\)
\(B=\dfrac{3.3.4.4.5.5.....21.21.22.22}{2.4.3.5.4.6.....20.22.21.23}\)
\(B=\dfrac{3.4.5.....21.22}{2.3.4.....20.21}.\dfrac{3.4.5.....21.22}{4.5.6.....22.23}\)
\(B=11.\dfrac{3}{23}=\dfrac{33}{23}\)
B = \(\dfrac{4}{3}.\dfrac{9}{8}.\dfrac{16}{15}.\dfrac{25}{24}...\dfrac{121}{120}.\dfrac{144}{143}\)
B = \(\dfrac{4.9.16.25...121.144}{3.8.15.24....120.143}\)
B = \(\dfrac{2.2.3.3.4.4.5.5...11.11.12.12}{1.3.2.4.3.5.4.6...10.12.11.13}\)
B = \(\dfrac{2.3.4.5...11.12}{1.2.3.4.5...10.11}.\dfrac{2.3.4.5...11.12}{3.4.5.6.7...12.13}\)
B = 12 . \(\dfrac{2}{13}\)
B = \(\dfrac{24}{13}\)

\(A=11\dfrac{3}{13}-\left(2\dfrac{4}{7}+5\dfrac{3}{13}\right)\)
\(A=11\dfrac{3}{13}-5\dfrac{3}{13}-2\dfrac{4}{7}\)
\(A=6-2\dfrac{4}{7}\)
\(A=5\dfrac{7}{7}-2\dfrac{4}{7}\)
\(A=3\dfrac{3}{7}\)
\(B=\left(6\dfrac{4}{9}+3\dfrac{7}{11}\right)-4\dfrac{4}{9}\)
\(B=\left(6\dfrac{4}{9}-4\dfrac{4}{9}\right)+3\dfrac{7}{11}\)
\(B=2+3\dfrac{7}{11}\)
\(B=5\dfrac{7}{11}\)
\(C=\dfrac{-5}{7}.\dfrac{2}{11}+\dfrac{-5}{7}-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{-5}{7}.\left(\dfrac{2}{11}+1\right)-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{-5}{7}.\dfrac{13}{11}-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{-65}{77}-\dfrac{9}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{4}{11}+1\dfrac{5}{7}\)
\(C=\dfrac{160}{11}\)
\(D=0,7.2\dfrac{2}{3}.20.0,375.\dfrac{5}{28}\)
\(D=\dfrac{7}{10}.\dfrac{8}{3}.20.\dfrac{375}{1000}.\dfrac{5}{28}\)
\(D=\dfrac{7}{28}=\dfrac{5}{2}\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{3}-0,25-\dfrac{1}{12}\right)\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{3}-\dfrac{1}{4}-\dfrac{1}{12}\right)\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right)\left(\dfrac{1}{12}-\dfrac{1}{12}\right)\)
\(E=\left(-6,17+3\dfrac{5}{9}-2\dfrac{36}{97}\right).0\)
\(\Rightarrow E=0\)

Gợi ý: Sử dụng tính chất phân phối của phép nhân đối với phép cộng để nhóm thừa số chung ra ngoài.

a: \(=\dfrac{5\cdot\left(8-6\right)}{10}=\dfrac{5\cdot2}{10}=1\)
b: \(\dfrac{\left(-4\right)^2}{5}=\dfrac{16}{5}\)
\(B=\dfrac{3}{7}-\dfrac{1}{5}-\dfrac{3}{7}=-\dfrac{1}{5}\)
c: \(C=\left(6-2.8\right)\cdot\dfrac{25}{8}-\dfrac{8}{5}\cdot4\)
\(=\dfrac{16}{5}\cdot\dfrac{25}{8}-\dfrac{32}{5}\)
\(=5\cdot2-\dfrac{32}{5}=10-\dfrac{32}{5}=\dfrac{18}{5}\)
d: \(D=\left(\dfrac{-5}{24}+\dfrac{18}{24}+\dfrac{14}{24}\right):\dfrac{-17}{8}\)
\(=\dfrac{27}{24}\cdot\dfrac{-8}{17}=\dfrac{-9}{8}\cdot\dfrac{8}{17}=\dfrac{-9}{17}\)

1/ \(B=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{8^2}\)
\(B< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{7.8}\)
\(B< \dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{7}-\dfrac{1}{8}\)
\(B< \dfrac{1}{1}-\dfrac{1}{8}< 1\)
\(B< 1\)
2/ \(B=\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{4}\right)...\left(1-\dfrac{1}{20}\right)\)
\(B=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}\cdot...\cdot\dfrac{19}{20}\)
\(B=\dfrac{1\times2\times3\times...\times19}{2\times3\times4\times...\times20}\)
\(B=\dfrac{1}{20}\)
3/ \(A=\dfrac{7}{4}\cdot\left(\dfrac{3333}{1212}+\dfrac{3333}{2020}+\dfrac{3333}{3030}+\dfrac{3333}{4242}\right)\)
\(A=\dfrac{7}{4}\cdot\left(\dfrac{33}{12}+\dfrac{33}{20}+\dfrac{33}{30}+\dfrac{33}{42}\right)\)
\(A=\dfrac{7}{4}\cdot\left(\dfrac{33}{3.4}+\dfrac{33}{4.5}+\dfrac{33}{5.6}+\dfrac{33}{6.7}\right)\)
\(A=\dfrac{7}{4}.33.\left(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}\right)\)
\(A=\dfrac{231}{4}.\left(\dfrac{1}{3}-\dfrac{1}{7}\right)\)
\(A=\dfrac{231}{4}\cdot\dfrac{4}{21}\)
\(A=11\)
4/ A phải là \(\dfrac{2011+2012}{2012+2013}\)
Ta có : \(B=\dfrac{2011}{2012}+\dfrac{2012}{2013}>\dfrac{2011}{2013}+\dfrac{2012}{2013}=\dfrac{2011+2012}{2013}>\dfrac{2011+2012}{2012+2013}=A\)
\(\Rightarrow B>A\)

a: \(=\dfrac{157}{8}\cdot\dfrac{12}{7}-\dfrac{61}{4}\cdot\dfrac{12}{7}\)
\(=\dfrac{12}{7}\left(\dfrac{157}{8}-\dfrac{122}{8}\right)\)
\(=\dfrac{12}{7}\cdot\dfrac{35}{8}=5\cdot\dfrac{3}{2}=\dfrac{15}{2}\)
b: \(=\dfrac{2}{15}-\dfrac{2}{15}\cdot5+\dfrac{3}{15}\)
\(=\dfrac{1}{3}-\dfrac{2}{3}=-\dfrac{1}{3}\)
c: \(=\left(\dfrac{10}{3}+\dfrac{5}{2}\right):\left(\dfrac{19}{6}-\dfrac{21}{5}\right)-\dfrac{11}{31}\)
\(=\dfrac{35}{6}:\dfrac{-31}{30}-\dfrac{11}{31}\)
\(=\dfrac{35}{6}\cdot\dfrac{30}{-31}-\dfrac{11}{31}\)
\(=\dfrac{-35\cdot5-11}{31}=\dfrac{-186}{31}=-6\)
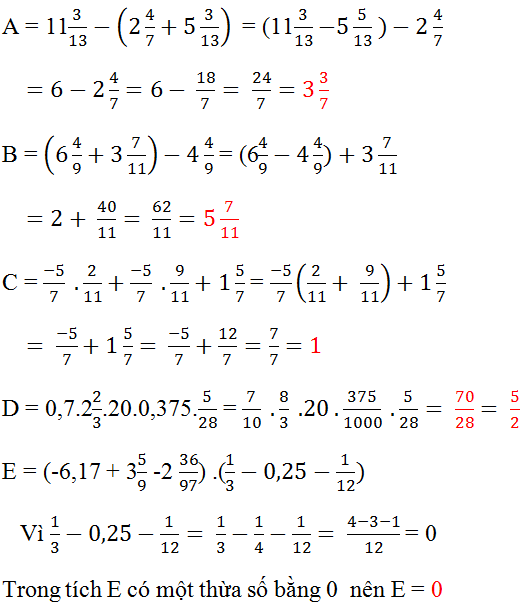
\(\left(\dfrac{1}{200}+\dfrac{1}{300}+\dfrac{1}{400}+...+\dfrac{1}{1000}\right).1.2.3.4.5\).\(\left(\dfrac{1}{120}-\dfrac{1}{180}-\dfrac{1}{360}\right)\)
Xét \(\left(\dfrac{1}{120}-\dfrac{1}{180}-\dfrac{1}{360}\right)\) ta có :
= \(\dfrac{1}{120}-\left(\dfrac{1}{180}+\dfrac{1}{360}\right)\) =\(\dfrac{1}{120}-\dfrac{1}{120}=0\)
Trong 1 tích nếu có 1 thừa số 0 thì tích đó bằng 0
Biểu thức trên có 1 thừa số 0 nên biểu thức trên bằng 0