
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
Ta thấy: $(x+\frac{1}{2})^2\geq 0$ với mọi $x\in\mathbb{R}$
$\Rightarrow (x+\frac{1}{2})^2+\frac{5}{4}\geq \frac{5}{4}$
Vậy gtnn của biểu thức là $\frac{5}{4}$
Giá trị này đạt tại $x+\frac{1}{2}=0\Leftrightarrow x=-\frac{1}{2}$
Bài 2:
$x+y-3=0\Rightarrow x+y=3$
\(M=x^2(x+y)-(x+y)x^2-y(x+y)+4y+x+2019\)
\(=-3y+4y+x+2019=x+y+2019=3+2019=2022\)

b) Thay x=-1; y=1 và z=-2 vào B, ta được:
\(B=\dfrac{3\cdot\left(-1\right)\cdot1\cdot\left(-2\right)-2\cdot\left(-2\right)^2}{\left(-1\right)^2+1}=\dfrac{6-8}{1+1}=\dfrac{-2}{2}=-1\)

a. *Thay x = 1 vào biểu thức, ta có: 12 – 5.1 = 1 – 5 = -4
Vậy giá trị của biểu thức x2 – 5x tại x = 1 là -4.
*Thay x = -1 vào biểu thức, ta có: (-1)2 – 5.(-1) = 1 + 5 = 6
Vậy giá trị của biểu thức x2 – 5x tại x = 1 là 6.
*Thay x = 1/2 vào biểu thức, ta có:
Vậy giá trị của biểu thức x2 – 5x tại x = 1/2 là -9/4 .
b. Thay x = -3 và y = -5 vào biểu thức, ta có:
3.(-3)2 – (-3)(-5) = 3.9 – 15 = 12
Vậy giá trị của biểu thức 3x2 – xy tại x = -3; y = -5 là 12.
c. Thay x = 1, y = -3 vào biểu thức, ta có:
5 – 1.(-3)3 = 5 – 1.(-27) = 5 + 27 = 32
Vậy giá trị của biểu thức 5 – xy3 tại x = 1; y = -3 là 32.
a) Thay x = 1 vào biểu thức ta có:
12−5.1=1−5=−412−5.1=1−5=−4
Vậy giá trị của biểu thức x2−5xx2−5x tại x = 1 là -4
Thay x = -1 vào biểu thức ta có:
(−1)2−5.(−1)=1+5=6(−1)2−5.(−1)=1+5=6
Vậy giá trị của biểu thức x2−5xx2−5x tại x = -1 là 6
Thay x=12x=12 vào biểu thức ta có:
(12)2−5.12=14−104=−94(12)2−5.12=14−104=−94
Vậy giá trị của biểu thức x2−5xx2−5x tại x=12x=12 là −94−94
b) Thay x = -3 và y = - 5 vào biểu thức ta có:
3.(−3)2−(−3).(−5)=3.9−15=123.(−3)2−(−3).(−5)=3.9−15=12
Vậy giá trị của biểu thức 3x2−xy3x2−xy tại x = -3; y = -5 là 12
c) Thay x = 1, y = -2 vào biểu thức ta có:
5−1.(−3)3=5−1.(−27)=5+27=325−1.(−3)3=5−1.(−27)=5+27=32
Vậy giá trị của biểu thức 5−xy35−xy3 tại x = 1; y = -3 là 32

a: \(A=5\cdot2\cdot\left(-3\right)-10+3\cdot\left(-3\right)=-30-10-9=-49\)
b: \(B=8\cdot1\cdot\left(-1\right)^2-1\cdot\left(-1\right)-2\cdot1-10\)
=8+1-2-10
=-3

Thay `x=\sqrt{3}` và `y=-1` vào `A`, ta được:
\(A=\left(\sqrt{3}\right)^2-\left|\left(\sqrt{3}\right)^2-\left(-1\right)\right|+2023\)
\(A=3-\left|3+1\right|+2023\)
\(A=3-4+2023\) ( vì `3+1>0` )
\(A=2022\)
Tại \(x=\sqrt{3};y=-1\) giá trị của biểu thức là:
\(A=\sqrt{3}^2-\left|\sqrt{3}^2-\left(-1\right)^2\right|+2023=3-\left|3+1\right|+2023=3-4+2023=2022\)

a: A=5x^2y-5x^2y-3xy+2xy+xy+x^4y^2+1+x^2
=x^4y^2+x^2+1
Khi x=-1 và y=1 thì A=(-1)^4*1^2+(-1)^2+1=3
b: A=x^2(x^2y^2+1)+1>=1>0 với mọi x,y
=>A luôn dương với mọi x,y
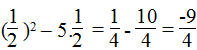
A=x(x+y-1)+2019
=>A=x.9+2019=2019
(do x+y=1)