
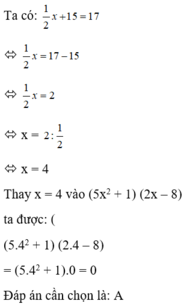
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

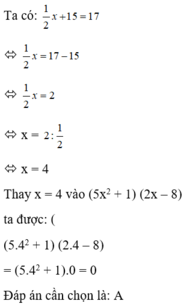

\(P=\left(\frac{x-1}{x+3}+\frac{2}{x-3}+\frac{x^2+3}{9-x^2}\right):\left(\frac{2x-1}{2x+1}-1\right)\)\(\left(đkcđ:x\ne\pm3;x\ne-\frac{1}{2}\right)\)
\(=\left(\frac{\left(x-1\right).\left(x-3\right)+2.\left(x+3\right)-\left(x^2+3\right)}{x^2-9}\right):\left(\frac{2x-1-\left(2x+1\right)}{2x+1}\right)\)
\(=\frac{x^2-4x+3+2x+6-x^2-3}{x^2-9}:\frac{-2}{2x+1}\)
\(=\frac{-2x-6}{x^2-9}.\frac{2x+1}{-2}\)
\(=\frac{-2\left(x+3\right)}{\left(x-3\right).\left(x+3\right)}.\frac{2x+1}{-2}\)
\(=\frac{2x+1}{x-3}\)
b)\(\left|x+1\right|=\frac{1}{2}\Leftrightarrow\orbr{\begin{cases}x+1=\frac{1}{2}\\x+1=-\frac{1}{2}\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-\frac{1}{2}\left(koTMđkxđ\right)\\x=-\frac{3}{2}\left(TMđkxđ\right)\end{cases}}}\)
thay \(x=-\frac{3}{2}\) vào P tâ đc: \(P=\frac{2x+1}{x-3}=\frac{2.\left(-\frac{3}{2}\right)+1}{-\frac{3}{2}-3}=\frac{4}{9}\)
c)ta có:\(P=\frac{x}{2}\Leftrightarrow\frac{2x+1}{x-3}=\frac{x}{2}\)
\(\Rightarrow2.\left(2x+1\right)=x.\left(x-3\right)\)
\(\Leftrightarrow4x+2=x^2-3x\)
\(\Leftrightarrow x^2-7x-2=0\)
\(\Leftrightarrow x^2-2.\frac{7}{2}+\frac{49}{4}-\frac{57}{4}=0\)
\(\Leftrightarrow\left(x-\frac{7}{2}\right)^2-\frac{57}{4}=0\)
\(\Leftrightarrow\left(x-\frac{7}{2}-\frac{\sqrt{57}}{2}\right).\left(x-\frac{7}{2}+\frac{\sqrt{57}}{2}\right)\)
bạn tự giải nốt nhé!!
d)\(x\in Z;P\in Z\Leftrightarrow\frac{2x+1}{x-3}\in Z\Leftrightarrow\frac{2x-6+7}{x-3}=2+\frac{7}{x-3}\in Z\)
\(2\in Z\Rightarrow\frac{7}{x-3}\in Z\Leftrightarrow x-3\inƯ\left(7\right)=\left\{\pm1;\pm7\right\}\)
bạn tự làm nốt nhé
a, \(\left(\dfrac{x^2-4x+3+2x+6-x^2-3}{\left(x+3\right)\left(x-3\right)}\right):\left(\dfrac{2x-1-2x-1}{2x+1}\right)\)
\(=\dfrac{-2x+6}{\left(x+3\right)\left(x-3\right)}:\dfrac{-2}{2x+1}=\dfrac{-2\left(x-3\right)\left(2x+1\right)}{-2\left(x+3\right)\left(x-3\right)}=\dfrac{2x+1}{x+3}\)
b, \(\left|x+1\right|=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}-1\\x=-\dfrac{1}{2}-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\left(ktmđk\right)\\x=-\dfrac{3}{2}\end{matrix}\right.\)
Thay x = -3/2 ta được \(\dfrac{2\left(-\dfrac{3}{2}\right)+1}{-\dfrac{3}{2}+3}=\dfrac{-2}{\dfrac{3}{2}}=-\dfrac{4}{3}\)

\(A=\left(x-4\right)^2-\left(x+4\right)^2-16\left(x-2\right)\)
\(=x^2-8x+16-x^2-8x-16-16x+32\)
\(=-32x+32\)
Biểu thức phụ thuộc vào giá trị của biến

a) \(8-\left|3x-5\right|=-14\)
\(\Rightarrow\left|3x-5\right|=22\)
\(\Rightarrow TH1:3x-5=22\Rightarrow x=9\)
\(TH2:3x-5=-22\Rightarrow x=\frac{-17}{3}\)
Vậy......
mấy câu kia tương tự

2: a) \(x^2-6x+2018\)
\(=\left(x^2-6x+9\right)+2009\)
\(=\left(x-3\right)^2+2009\)
Vì \(\left(x-3\right)^2\ge0\forall x\) ; \(2009>0\) nên \(\left(x-3\right)^2+2009>0\forall x\)
Hay \(x^2-6x+2018>0\forall x\) \(\left(dpcm\right)\)
b) \(4x-x^2-5\)
\(=-\left(x^2-4x+5\right)\)
\(=-\left[\left(x^2-4x+4\right)+1\right]\)
\(=-\left(x-2\right)^2-1\)
Vì \(\left(x-2\right)^2\ge0\forall x\) nên \(-\left(x-2\right)^2\le0\forall x\)
\(\Rightarrow-\left(x-2\right)^2-1< 0\)
Hay \(4x-x^2-5< 0\forall x\) \(\left(dpcm\right)\)
Bài 3:
\(A=2\left(x^2-3x\right)=2\left(x^2-2.x.\frac{3}{2}+\frac{9}{4}-\frac{9}{4}\right)\)
\(=2\left(x-\frac{3}{2}\right)^2-\frac{9}{2}\ge-\frac{9}{2}\)
Đẳng thức xảy ra khi x = 3/2
\(B=\left(x^2-x+\frac{1}{4}\right)+\left(y^2+6y+9\right)+1\)
\(=\left(x-\frac{1}{2}\right)^2+\left(y+3\right)^2+1\ge1\)
Đẳng thức xảy ra khi x = 1/2 y = -3

Mk xin lỗi nha, câu c sai đề
c) (x+6)4 + (x+8)4 = 272

\(A=x^2-3x+5\)
\(=x^2-3x+\frac{9}{4}+\frac{11}{4}\)
\(=\left(x-\frac{3}{2}\right)^2+\frac{11}{4}\)
\(\left(x-\frac{3}{2}\right)^2\ge0\Rightarrow A\ge\frac{11}{4}\)
Dấu "=" xảy ra khi \(x-\frac{3}{2}=0\Rightarrow x=\frac{3}{2}\)
Vậy Min A = \(\frac{11}{4}\Leftrightarrow x=\frac{3}{2}\)
a) \(A=x^2-3x+5\)
\("="\Leftrightarrow x=\frac{11}{4}\Rightarrow x=\frac{3}{2};\frac{11}{4}\)
b) \(B=\left(2x-1\right)^2+\left(x+2\right)^2\)
\("="\Leftrightarrow x=5\Rightarrow x=0;5\)
c) \(C=4x-x^2+3\)
\("="\Leftrightarrow x=7\Rightarrow x=2;7\)
d) \(D=x^4+x^2+2\)
\("="\Leftrightarrow x=2\Rightarrow x=0;2\)

$a)\dfrac{3{{x}^{2}}+7x-10}{x}=0$
ĐK: $x\ne 0$
$\begin{align}
& Pt\Leftrightarrow 3{{x}^{2}}-3x+10x-10=0 \\
& \Leftrightarrow 3x\left( x-1 \right)+10\left( x-1 \right)=0 \\
& \Leftrightarrow \left( x-1 \right)\left( 3x+10 \right)=0 \\
& \Leftrightarrow \left[ \begin{align}
& x-1=0 \\
& 3x+10=0 \\
\end{align} \right.\Leftrightarrow \left[ \begin{align}
& x=1 \\
& x=-\dfrac{10}{3} \\
\end{align} \right.\left( tm \right) \\
\end{align}$
$b)\dfrac{4x-17}{2{{x}^{2}}+1}=0$
ĐK: $x\in \mathbb{R}$
$Pt\Leftrightarrow 4x-17=0\Rightarrow x=\dfrac{17}{4}\left( tm \right)$

bài này đề bài là chứng minh hay là giải bất phương trình vậy bạn