Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a). Đường kính OA của hình tròn tâm M và đường kính OB của hình tròn tâm N là :
8:2=4(cm)
Chu vi hình tròn tâm M là :
4×3,14=12,56 (cm)
Chu vi hình tròn tâm N là:
4×3,14=12,56 (cm)
Chu vi hình tròn tâm O là :
8×3,14=25,12 (cm)
b. Tổng chu vi hình tròn tâm M và hình tròn tâm N là:
12,56+12,56=25,12 (cm)
Vậy tổng chu vi hình tròn tâm M và hình tròn tâm N bằng chu vi hình tròn tâm O.
c) Diện tích hình tròn tâm O đường kính AB là:
4×4×3,14=50,24(cm2)4×4×3,14=50,24(cm2)
Tổng diện tích đường tròn tâm M và tâm N là:
(4:2)×(4:2)×3,14×2=25,12(cm2)(4:2)×(4:2)×3,14×2=25,12(cm2)
Diện tích phần tô đậm là:
50,24−25,12=25,12(cm2)50,24−25,12=25,12(cm2)
Đáp số:b) bằng nhau, c) 25,12cm2

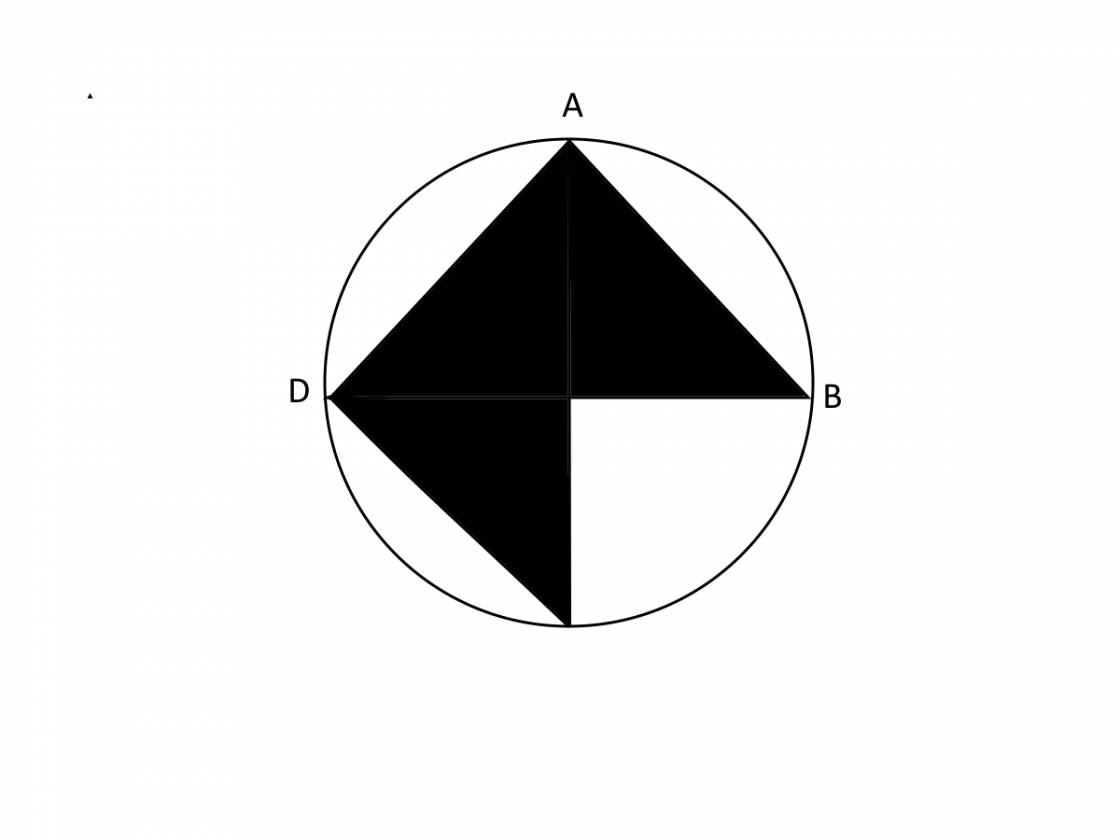
Bán kính hình tròn là:
\(15,7:\left(2\times3,14\right)=2,5\left(m\right)\)
Phần tô đậm được tạo thành từ ba tam giác vuông cân có diện tích bằng nhau, trong đó mỗi tam giác có cạnh góc vuông bằng bán kính hình tròn, do đó diện tích hình tô đậm là:
\(3\times2,5\times2,5:2=9,375\left(m^2\right)\)
Bán kính hình tròn là:
15,7:(2×3,14)=2,5(�)15,7:(2×3,14)=2,5(m)
Phần tô đậm được
Bán kính hình tròn là:
15,7:(2×3,14)=2,5(�)15,7:(2×3,14)=2,5(m)
Phần tô đậm được tạo thành từ ba tam giác vuông cân có diện tích bằng nhau, trong đó mỗi tam giác có cạnh góc vuông bằng bán kính hình tròn, do đó diện tích hình tô đậm là:
3×2,5×2,5:2=9,375(�2)3×2,5×2,5:2=9,375(m2)
2=9,375(m

Cho 3 hình tròn như hình vẽ.các hình tròn tâm o1 và tâm o2 có bán kính là 0,3 dm và 0,5 dm.a)tính bán kính của hình tròn tâm O.b)tính diện tích qhần tô màu đậm của hình tròn tâm O
Bạn ơi, không có hình thì làm sao biết phần gạch đậm chỗ nào??!!!
bạn cho hình ik ...chụp lại bn nờ