Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

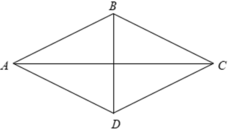
Gọi H là giao điểm của hai đường chéo AC,BD.
Theo giải thiết ta có: AC + BD = 46( cm )
⇔ ( HB + HD ) + ( HC + HA ) = 46
⇔ 2HB + 2HA = 46 ⇔ HA + HB = 23
Khi đó ta có: HA + HB = 23


gọi O là giao điểm của hai đường chéo AC và BD
Đặt OA=x,OB=y,ta có x+y=23 và x^2+y^2=17^2=289
Diện tích hình thoi ABCD=1/2 (AC.BD )=1/2 ( 2x.2y) =2xy
Từ x+y =23 mà (x+y)^2 =529
suy ra x^2 +2xy+y^2 =529
2xy+289=529
2xy =240
Vậy diện tích hình thoi ABCD là 240 cm^2
diện tích tam giác là :
23 . 23 : 2 = 264 . 5 ( cm2)
đáp số : ..................................

Đặt OA = x và OB =y, ta có:
S A B C D = 1 2 A C . B D = 1 2 2 x .2 y = 2 x y
Theo giả thiết, ta có: 2 ( x + y ) = 46 x 2 + y 2 = 17 2 = 289
Þ 2xy =240 Þ SABCD = 240cm2

Gọi độ dài đường chéo thứ nhất là x
Độ dài đường chéo thứ hai là 34-x
Theo đề, ta có: x(34-x)=240
\(\Leftrightarrow34x-x^2-240=0\)
\(\Leftrightarrow x^2-34x+240=0\)
\(\Leftrightarrow\left(x-10\right)\left(x-24\right)=0\)
=>x=10 hoặc x=24
Vậy: Độ dài cạnh là \(\sqrt{\left(\dfrac{10}{2}\right)^2+\left(\dfrac{24}{2}\right)^2}=\sqrt{5^2+12^2}=13\left(m\right)\)

Gọi độ dài đường chéo thứ nhất của hình thoi là \(m\left(0< m< 34\right)\)
Khi đó do tổng độ dài 2 đường chéo là 34m nên độ dài đường chéo thứ hai là \(34-m\)
Diện tích hình thoi là 120m2 nên ta có phương trình \(\frac{m\left(34-m\right)}{2}=120\)\(\Leftrightarrow m\left(34-m\right)=240\)\(\Leftrightarrow-m^2+34m=240\)\(\Leftrightarrow m^2-34m+240=0\)\(\Leftrightarrow m^2-10m-24m+240=0\)\(\Leftrightarrow m\left(m-10\right)-24\left(m-10\right)=0\)\(\Leftrightarrow\left(m-10\right)\left(m-24\right)=0\)\(\Leftrightarrow\orbr{\begin{cases}m-10=0\\m-24=0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}m=10\\m=24\end{cases}}\)(nhận)
Vậy độ dài hai đường chéo lần lượt là 10m, 24m
Gọi H là giao điểm của hai đường chéo AC,BD.
Theo giải thiết ta có: AC + BD = 46( cm )
⇔ ( HB + HD ) + ( HC + HA ) = 46
⇔ 2HB + 2HA = 46 ⇔ HA + HB = 23
Khi đó ta có