Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
E =16+112+120+130+142+156
E=\(\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}\)
E=\(\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{1}-...+\dfrac{1}{7}-\dfrac{1}{8}\)
E=\(\dfrac{1}{2}-\dfrac{1}{8}=\dfrac{3}{8}\)
`[-1]/2+[-1]/6+[-1]/12+[-1]/20+[-1]/30+[-1]/42+[-1]/56+[-1]/72+[-1]/90`
`=(-1)(1/2+1/6+1/12+1/20+1/30+1/42+1/56+1/72+1/90)`
`=(-1)(1-1/2+1/2-1/3+1/3-1/4+1/4-1/5+1/5-1/6+1/6-1/7+1/7-1/8+1/8-1/9+1/9-1/10)`
`=(-1)(1-1/10)`
`=(-1). 9/10=-9/10`
A = \(\dfrac{-1}{2}\) + \(\dfrac{-1}{6}\)+ \(\dfrac{-1}{12}\)+ \(\dfrac{-1}{20}\)+ \(\dfrac{-1}{30}\)+ \(\dfrac{-1}{42}\)+ \(\dfrac{-1}{56}\)+ \(\dfrac{-1}{72}\)+ \(\dfrac{-1}{90}\)
A = \(\dfrac{-1}{2}\) + \(\dfrac{-1}{2\times3}\)+ \(\dfrac{-1}{3\times4}\)+ \(\dfrac{-1}{4\times5}\)+ \(\dfrac{-1}{5\times6}\)+ \(\dfrac{-1}{6\times7}\)+ \(\dfrac{-1}{7\times8}\)+ \(\dfrac{-1}{8\times9}\)+ + \(\dfrac{-1}{9\times10}\)
A = - (\(\dfrac{1}{2}\)+ \(\dfrac{1}{2}\)-\(\dfrac{1}{3}\)+ \(\dfrac{1}{3}\)-\(\dfrac{1}{4}\)+ \(\dfrac{1}{4}\)- \(\dfrac{1}{5}\)+ \(\dfrac{1}{5}\)-\(\dfrac{1}{6}\)+ \(\dfrac{1}{6}\)-\(\dfrac{1}{7}\)+\(\dfrac{1}{7}\)-\(\dfrac{1}{8}\)+\(\dfrac{1}{8}\)-\(\dfrac{1}{9}\)+ \(\dfrac{1}{9}\)-\(\dfrac{1}{10}\))
A = -(1-\(\dfrac{1}{10}\))
A = \(\dfrac{-9}{10}\)
=9/10-(1/2+1/6+...+1/90)
=9/10-(1-1/2+1/2-1/3+...+1/9-1/10)
=9/10-9/10=0
Quãng sông AB dài là :
8 giờ 24 phú x 10 = 84 (km)
Vận tốc cua ca nô khi xuôi dòng là :
10 + 2 = 12 (km/giờ )
Thời gian ca nô đi xuôi dòng là :
84 : 2 = 7 (giờ )
Đáp số : 7 giờ
dễ mà
\(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}\)
\(=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+\dfrac{1}{4\cdot5}+\dfrac{1}{5\cdot6}+\dfrac{1}{6\cdot7}+\dfrac{1}{7\cdot8}+\dfrac{1}{8\cdot9}+\dfrac{1}{9\cdot10}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{10}\)
\(=1-\dfrac{1}{10}\)
\(=\dfrac{10}{10}-\dfrac{1}{10}=\dfrac{9}{10}\)
a) \(A=\dfrac{3}{5}+6\dfrac{5}{6}+\left(11\dfrac{5}{20}-9\dfrac{1}{4}\right):8\dfrac{1}{3}\)
\(=\dfrac{3}{5}+\dfrac{41}{6}\left(11\dfrac{1}{4}-9\dfrac{1}{4}\right):8\dfrac{1}{3}\)
\(=\dfrac{3}{5}+\dfrac{41}{6}.2.\dfrac{3}{25}\)
\(=\dfrac{3}{5}+\dfrac{41}{25}\)
\(=\dfrac{15}{25}+\dfrac{41}{25}\)
\(=\dfrac{56}{25}\)
a) A = \(\dfrac{3}{5}+6\dfrac{5}{6}\left(11\dfrac{5}{20}-9\dfrac{1}{4}\right):8\dfrac{1}{3}\)
A = \(\dfrac{3}{5}+\dfrac{41}{6}\) \(\left(\dfrac{45}{4}-\dfrac{37}{4}\right)\) : \(\dfrac{25}{3}\)
A = \(\dfrac{3}{5}+\dfrac{41}{6}\) . 2 : \(\dfrac{25}{3}\)
A = \(\dfrac{3}{5}\) + \(\dfrac{41}{3}\) : \(\dfrac{25}{3}\)
A = \(\dfrac{3}{5}\) + \(\dfrac{41}{25}\)
A = \(\dfrac{56}{25}\)
\(\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}\\ =\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+\dfrac{1}{8.9}\\ =\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}\\ =\dfrac{1}{3}-\dfrac{1}{9}\\ =\dfrac{2}{9}\)
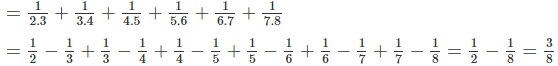
\(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}\)
\(=\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}\)
\(=1-\dfrac{1}{8}=\dfrac{7}{8}\)
Chúc bạn học tốt!!!