
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

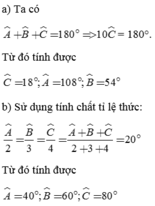

2) TA CÓ 1/22-1=(1/2-1)x(1/2+1)=-1/2x3/2
1/32-1=(1/3-1)x(1/3+1)=-2/3X4/3..............1/992-1=(1/99-1)(1/99+1)=-98/99x100/99;1/1002-1=(1/100-1)x(1/100+1)=-99/100x101/100
ta có A=-(1/2x2/3x.....98/99x99/100)x(3/2x4/3x......x100/99x101/100)=-1/100x101/2=-101/50<-1/2
TA CÓ 1/22-1=(1/2-1)X(1/2+1)=-1/2X3/2 ;1/32-1=(1/3-1)X(1/3+1)=-2/3X4/3.....................
1/992-1=(1/99-1)X(1/99+1)=-98/99X100/99 ;1/1002-1=(1/100-1)X(1/100+1)=99/100X101/100
VẬY A=-(1/2X2/3X.......X98/99X99/100)X(3/2X4/3X....X100/99X101/100)=-101/50<-1/2

2) \(A=\left(\frac{1}{2^2}-1\right).\left(\frac{1}{3^2}-1\right).\left(\frac{1}{4^2}-1\right)...\left(\frac{1}{100^2}-1\right)\)
\(A=\frac{-3}{2^2}.\frac{-8}{3^2}.\frac{-15}{4^2}...\frac{-9999}{100^2}\)
\(A=-\left(\frac{3}{2^2}.\frac{8}{3^2}.\frac{15}{4^2}...\frac{9999}{100^2}\right)\) (vì có 99 thừa số âm nên kết quả là âm)
\(A=-\left(\frac{1.3}{2.2}.\frac{2.4}{3.3.}.\frac{3.5}{4.4}...\frac{99.101}{100.100}\right)\)
\(A=-\left(\frac{1.2.3...99}{2.3.4...100}.\frac{3.4.5...101}{2.3.4...100}\right)\)
\(A=-\left(\frac{1}{100}.\frac{101}{2}\right)\)
\(A=-\frac{101}{200}< -\frac{100}{200}=-\frac{1}{2}\)
Trả lời câu nào cũng được nha mấy bạn! Help me, please!!!!!!! ![]()
![]()

a2 = bc
\(\Rightarrow a.a=b.c\Rightarrow\frac{a}{b}=\frac{c}{a}\Rightarrow\frac{a}{c}=\frac{b}{a}\)
Áp dụng tính chất dãy tỉ số bằng nhau , ta có :
\(\frac{a}{c}=\frac{b}{a}=\frac{a+b}{c+a}=\frac{a-b}{c-a}\)
\(\Rightarrow\frac{a+b}{a-b}=\frac{c+a}{c-a}\)

Bài 2:
\(\widehat{ADB}=180^0-80^0=100^0\)
Ta có: \(\widehat{ADB}+\widehat{BAD}+\widehat{B}=\widehat{ADC}+\widehat{CAD}+\widehat{C}\)
\(\Leftrightarrow\widehat{B}+100^0=\widehat{C}+80^0\)
\(\Leftrightarrow1.5\widehat{C}-\widehat{C}=-20^0\)
\(\Leftrightarrow\widehat{C}=40^0\)
hay \(\widehat{B}=60^0\)
=>\(\widehat{BAC}=80^0\)

Bài 2:
Đặt số đo góc B là x, số đo góc C là y
Theo đề, ta có:
\(\left\{{}\begin{matrix}x+y=90\\x-y=24\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=114\\x+y=90\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=57^0\\y=33^0\end{matrix}\right.\)

Theo đề bài suy ra \(\hept{\begin{cases}\frac{A}{3}=\frac{B}{1}\\\frac{B}{1}=\frac{C}{2}\end{cases}}\Rightarrow\frac{A}{3}=\frac{B}{1}=\frac{C}{2}\)
Áp dụng tính chất dãy tỉ số bằng nhau: \(\frac{\widehat{A}}{3}=\frac{\widehat{B}}{1}=\frac{\widehat{C}}{2}=\frac{\widehat{A}+\widehat{B}+\widehat{C}}{3+1+2}=\frac{180^o}{6}=30^o\)
Suy ra...


Gọi \(\widehat{A}:\widehat{B}:\widehat{C}\)lần lượt là a,b,c
Do \(\widehat{A}:\widehat{B}:\widehat{C}=3:4:5\)
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}\)
Mà tổng \(\widehat{A}:\widehat{B}:\widehat{C}=180^o\)(tổng 3 góc trong tam giác)
=>\(\frac{a+b+c}{3+4+5}=\frac{180}{12}=15\)
\(\Rightarrow\hept{\begin{cases}\frac{a}{3}\\\frac{b}{4}\\\frac{c}{5}\end{cases}}=15\)
\(\Rightarrow\hept{\begin{cases}a=45^o\\b=60^o\\c=75^o\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\widehat{A}=45^o\\\widehat{B}=60^o\\\widehat{C}=75^o\end{cases}}\)
MÀ \(\Delta ABC=\Delta A'B'C'\)
\(\Rightarrow\hept{\begin{cases}\widehat{A}=\widehat{A'}\\\widehat{B}=\widehat{B'}\\\widehat{C}=\widehat{C'}\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}\widehat{A'=45^o}\\\widehat{B'=60^o}\\\widehat{C'}=75^o\end{cases}}\)
Đặt: \(\widehat{A}=3x\Rightarrow\hept{\begin{cases}\widehat{B}=4x\\\widehat{C}=5x\end{cases}}\)
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
\(\Rightarrow3x+4x+5x=180^o\)
\(\Rightarrow x=15\)
\(\Rightarrow\hept{\begin{cases}\widehat{A'}=\widehat{A}=3x=45^o\\\widehat{B}'=\widehat{B}=4x=60^o\\\widehat{C'}=\widehat{C}=75^o\end{cases}}\)