Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) góc BED nội tiếp chắn nửa đg tròn đg kính BD => góc BED =900 hay góc BEC =900
=> góc BEC = góc BAC = 900 => tứ giác ACBE nội tiếp đg tròn đg kính BC, tâm G là trung điểm BC
b) tứ giác ACBE nội tiếp => góc ABC = góc AEC (1)
mặt khác B,D,E,F thuộc đg tròn đg kính BD => BDEF là tứ giác nội tiếp => góc AED = góc DBF (góc ngoài bằng góc đối trog)
hay góc AEC = góc ABF (2)
từ (1) và (2) => đpcm
c) trog (G) góc AGB = 2 góc ACB (góc nội tiếp và góc ở tâm) => góc AGB = 1200 => sđ cung AB = 1200
mặt khác tam giác AGC đều nên GA =3cm
từ đó bn tính đc S quạt AGBA = \(27\pi\left(cm^2\right)\)

Bạn tự vẽ hình nhé !
Gọi\(\Delta ABC\)đều có O vừa là tâm đường tròn ngoại tiếp vừa là trọng tâm ; AH vừa là đường cao vừa là trung tuyến
=> HB = BC/2 = 3/2 = 1,5 (cm) =>\(\Delta AHB\)vuông tại H có :\(AH=\sqrt{AB^2-BH^2}=\sqrt{3^2-\left(1,5\right)^2}=\frac{3\sqrt{3}}{2}\left(cm\right)\)
=> Bán kính đường tròn ngoại tiếp là : AO =\(\frac{2}{3}.AH=\frac{2}{3}.\frac{3\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)(vì O là trọng tâm)

Áp dụng công thức Bài 46 ta có:
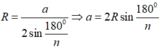
Áp dụng vào hình ngũ giác đều nội tiếp đường tròn bán kính 3cm ta có: