Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-1;y+3;-5\right)\\\overrightarrow{AC}=\left(x-2;7;-1\right)\end{matrix}\right.\)
\(A;B;C\) thẳng hàng \(\Rightarrow\frac{-1}{x-2}=\frac{y+3}{7}=\frac{-5}{-1}\)
\(\Rightarrow\left\{{}\begin{matrix}x-2=-\frac{1}{5}\\y+3=35\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=\frac{9}{5}\\y=32\end{matrix}\right.\) \(\Rightarrow10x+y=50\)

Bài làm
A = 1 giờ 24 phút + 1,4 giờ x 7 + 2 giờ 10 phút + 38 phút
A = 1,4 giờ + 1,4 giờ x 7 + 2 giờ 48 phút
A = 1,4 giờ + 1,4 giờ x 7 + 2,8 giờ
A = 1,4 giờ + 1,4 giờ x 7 + 1,4 giờ + 1,4 giờ
A = 1,4 giờ x ( 1 + 7 + 1 + 1 )
A = 1,4 giờ x 10
A = 14 giờ
Giải
1,4 giờ = 1 giờ 24 phút.
vậy ta có 1 giờ 24 phút + 1 giờ 24 phút x 7
= 1 giờ 24 phút x ( 7 + 1 )
= 1 giờ 24 phút x 8 2 giờ 10 phút + 38 phút
= 2 giờ 48 phút = 2 x 1 giờ 24 phút.
vậy ta có 1 giờ 24 phút x (8 + 2)
= 1 giờ 24 phút x 10 và 1 giờ 24 phút x 10
= 10 giờ 240 phút
= 14 giờ

Chọn A
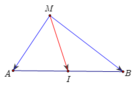
Gọi I, O lần lượt là trung điểm của AB và IC, khi đó với điểm M bất kỳ ta luôn có
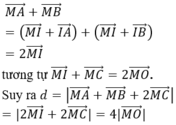
nên d nhỏ nhất khi và chỉ khi ![]() nên M là hình chiếu vuông góc của O lên (P). Có A(0; -2; -1), B (-2,-4,3) => I (-1 ; -3 ; 1), kết hợp với C (1; 3; -1) ta có O (0;0;0)
nên M là hình chiếu vuông góc của O lên (P). Có A(0; -2; -1), B (-2,-4,3) => I (-1 ; -3 ; 1), kết hợp với C (1; 3; -1) ta có O (0;0;0)
Đường thẳng qua O (0;0;0) vuông góc với (P) có phương trình 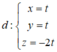
Giao điểm của d và (P) chính là hình chiếu vuông góc M của O (0;0;0) lên mặt phẳng (P).
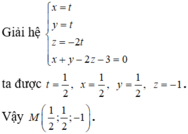

a) 72 x 212 + 27 x 121 + 121
= 72 x 212 + 27 x 121 + 121
= 72 x 212 + 27 x 121 + 121 x 1
= 72 x 212 + (27 + 1) x 121
= 72 x 212 + 28 x 121
= 72 x (121 + 91) + 28 x 121
= 72 x 121 + 72 x 91 + 28 x 121
= (72 + 28) x 121 + 72 x 91
= 100 x 121 + 72 x 91
= 12100 + 6552
= 18652 (anh thấy bài này sao ý)
b) (165 x 99 + 165) - ( 163 x 101 - 163)
= (165 x 99 + 165 x 1) - ( 163 x 101 - 163 x 1)
= [165 x (99 + 1)] - [163 x (101 - 1)]
= 165 x 100 - 163 x 100
= 16500 - 16300
= 200
c) 24 x 62 + 48 x 19
= 24 x 62 + (24 + 24) x 19
= 24 x 62 + 24 x 19 + 24 x 19
= 24 x (62 + 19 + 19)
= 24 x 100
= 2400
d) 24 x 76 + 48 x 12 - 20 x 100
= 24 x 76 + (24 + 24) x 12 - 20 x 100
= 24 x 76 + 24 x 12 + 24 x 12 - 20 x 100
= 24 x (76 + 12 + 12) - 20 x 100
= 24 x 100 - 20 x 100
= 100 x (24 - 20)
= 100 x 4
= 400
( nhớ tính lại xem đúng ko nha, anh lỡ có sai thì chết. Bài nào sai báo ngay cho anh )
HỌC TỐT ![]()




a) 41,25 x 99 + 41,25
= 41,25 x 99 + 41,25 +1
= 41,25 x ( 99 + 1 )
= 41,25 x 100
= 4125