PT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
18 tháng 11 2017
a. 32x - 5.(3.2)x + 22x.4 =0
(=) \(\left(\dfrac{3}{2}\right)^{^{2x}}-5.\left(\dfrac{3}{2}\right)^x+2^{2x}.4\) =0
đặt \(\left(\dfrac{3}{2}\right)^x=t\) đk: t > 0
=> pttt: t2 - 5t +4 =0
(=)\(\left[{}\begin{matrix}t=1\\t=4\end{matrix}\right.\)
(=) \(\left[{}\begin{matrix}\left(\dfrac{3}{2}\right)^x=1\\\left(\dfrac{3}{2}\right)^x=4\end{matrix}\right.\)
(=)\(\left[{}\begin{matrix}x=0\\x=\log_{\dfrac{3}{2}}4\end{matrix}\right.\)
18 tháng 11 2017
b. 3.52x + 2.72x - 5.(5.7)x =0
(=) \(3+2.\left(\dfrac{7}{5}\right)^{2x}-5.\left(\dfrac{7}{5}\right)^x=0\)
đặt \(t=\left(\dfrac{7}{5}\right)^x\) đk: t > 0
pttt: 3+2t2-5t=0
(=) \(\left[{}\begin{matrix}t=1\\t=\dfrac{3}{2}\end{matrix}\right.\)
(=)\(\left[{}\begin{matrix}x=0\\x=\log_{\dfrac{7}{5}}\dfrac{3}{2}\end{matrix}\right.\)
10 tháng 5 2016
\(C=\left(0,5\right)^{-4}-625^{0,25}-\left(2\frac{1}{4}\right)^{-1\frac{1}{2}}+19\left(-3\right)^{-3}=\left(2^{-1}\right)^{-4}-\left(5^4\right)^{\frac{1}{4}}-\left[\left(\frac{3}{2}\right)^2\right]^{-\frac{3}{2}}+19.\frac{1}{\left(-3\right)^3}\)
\(=2^4-5-\left(\frac{3}{2}\right)^{-3}-\frac{19}{27}\)
\(=11-\left(\frac{2}{3}\right)^3-\frac{19}{27}=10\)
10 tháng 5 2016
\(C=\left(0,5\right)^{-4}-625^{0,25}-\left(2\frac{1}{4}\right)^{-1\frac{1}{2}}+19.\left(-3\right)^{-3}\)
\(=\left(\frac{1}{2}\right)^{-4}-625^{\frac{1}{4}}-\left(\frac{9}{4}\right)^{-\frac{3}{2}}+19.\left(-3\right)^{-3}\)
\(=2^4-\sqrt[4]{625}-\left(\frac{4}{9}\right)^{\frac{3}{2}}+19.\left(\frac{1}{\left(-3\right)^3}\right)\)
=\(16-5-\sqrt[2]{\left(\frac{4}{9}\right)^3}+19.\frac{1}{-27}=11-\frac{8}{27}-\frac{19}{27}=10\)
GV
Giáo viên Toán
Giáo viên
26 tháng 4 2017
a) \(\left(\dfrac{1}{16}\right)^{-\dfrac{3}{4}}+810000^{0.25}-\left(7\dfrac{19}{32}\right)^{\dfrac{1}{5}}\)
\(=\left(\dfrac{1}{2}\right)^{4.\left(-\dfrac{3}{4}\right)}+\left(30\right)^{4.0,25}-\left(\dfrac{243}{32}\right)^{\dfrac{1}{5}}\)
\(=\left(\dfrac{1}{2}\right)^{-3}+30-\left(\dfrac{3}{2}\right)^{5.\dfrac{1}{5}}\)
\(=2^3+30-\dfrac{3}{2}\)
\(=36,5\)
GV
Giáo viên Toán
Giáo viên
26 tháng 4 2017
b) \(=\left(0,1\right)^{3.\left(-\dfrac{1}{3}\right)}-2^{-2}.2^{6.\dfrac{2}{3}}-\left[\left(2\right)^3\right]^{-\dfrac{4}{3}}\)
\(=0,1^{-1}-2^2-2^{-4}\)
\(=10-4-\dfrac{1}{16}\)
\(=\dfrac{95}{16}\)
PT
1
CM
25 tháng 5 2019
Chiều cao AH của tứ diện ABCD chính là khoảng cách từ điểm A đến mp (BCD) :
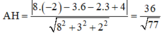
- 0 , 5 - 4 - 625 0 , 25 - 2 1 4 - 1 1 2 = 289 27