
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

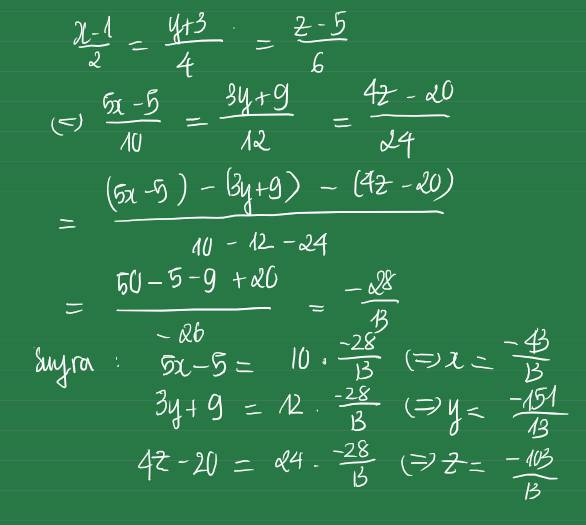

a) \(\dfrac{x^3}{8}=\dfrac{y^3}{64}=\dfrac{z^3}{216}\)
Từ \(\dfrac{x^3}{8}=\dfrac{y^3}{64}=\dfrac{z^3}{216}\Rightarrow\dfrac{x^3}{2^3}=\dfrac{y^3}{4^3}=\dfrac{z^3}{6^3}\)
\(\Leftrightarrow\dfrac{x^2}{2^2}=\dfrac{y^2}{4^2}=\dfrac{z^2}{6^2}\Leftrightarrow\dfrac{x^2}{4}=\dfrac{y^2}{16}=\dfrac{z^2}{36}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x^2}{4}=\dfrac{y^2}{16}=\dfrac{z^2}{36}=\dfrac{x^2+y^2+z^2}{4+16+36}=\dfrac{14}{56}=\dfrac{1}{4}\)
\(\Rightarrow\dfrac{x^2}{4}=\dfrac{1}{4}\Rightarrow x^2=\dfrac{1}{4}\cdot4\Rightarrow x^2=1\Rightarrow x=1\)
\(\dfrac{y^2}{16}=\dfrac{1}{4}\Rightarrow y^2=\dfrac{1}{4}\cdot16\Rightarrow y^2=4\Rightarrow y=2\)
\(\dfrac{z^2}{36}=\dfrac{1}{4}\Rightarrow z^2=\dfrac{1}{4}\cdot36\Rightarrow z^2=9\Rightarrow z^2=3\)
Xin lỗi mình chỉ làm được câu a)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\dfrac{x-1}{2}=\dfrac{y+3}{4}=\dfrac{z-5}{6}\)
\(\Rightarrow\dfrac{5z-25}{30}=\dfrac{3x-3}{6}=\dfrac{4y+12}{16}\\ =\dfrac{\left(5z-25\right)-\left(3x-3\right)-\left(4y+12\right)}{30-6-16}\\ =\dfrac{5z-25-3x+3-4y-12}{8}\\ =\dfrac{5z-3x-4y-34}{8}\\ \dfrac{50-34}{8}=2\\ \Rightarrow\left\{{}\begin{matrix}\dfrac{5z-25}{30}=2\\\dfrac{3x-3}{6}=2\\\dfrac{4y+12}{16}=2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}5z=85\\3x=15\\4y=20\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}z=17\\x=5\\y=5\end{matrix}\right.\)

\(x-y+100=z\Rightarrow x-y-z=-100\)
\(\dfrac{x}{4}=\dfrac{y}{3}\Rightarrow\dfrac{x}{20}=\dfrac{y}{15};\dfrac{y}{5}=\dfrac{z}{3}\Rightarrow\dfrac{y}{15}=\dfrac{z}{9}\)
\(\Rightarrow\dfrac{x}{20}=\dfrac{y}{15}=\dfrac{z}{9}=\dfrac{x-y-z}{20-15-9}=\dfrac{-100}{-4}=25\)
\(\Rightarrow x=20.25=500;y=15.25=375;z=9.25=225\)
b/ \(\dfrac{x-1}{2}=\dfrac{y+3}{4}=\dfrac{z-5}{6}\)
\(\Rightarrow\dfrac{3x-3}{6}=\dfrac{4y+12}{16}=\dfrac{5z-25}{30}=\dfrac{5z-25-4y-12-3x+3}{30-16-6}=2\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x-1}{2}=2\\\dfrac{y+3}{4}=2\\\dfrac{z-5}{6}=2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=5\\y=5\\z=17\end{matrix}\right.\)
c/ \(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{5}=a\Rightarrow\left\{{}\begin{matrix}x=2a\\y=3a\\z=5a\end{matrix}\right.\) \(\Rightarrow xyz=2a.3a.5a=30a^3=-30\Rightarrow a^3=-1\Rightarrow a=-1\)
\(\Rightarrow\left\{{}\begin{matrix}x=2a=-2\\y=3a=-3\\z=5a=-5\end{matrix}\right.\)
d/ \(\dfrac{x}{1,1}=\dfrac{y}{1,3}=\dfrac{z}{1,4}\Rightarrow\dfrac{2x}{2,2}=\dfrac{y}{1,3}=\dfrac{z}{1,4}=\dfrac{2x-y}{2,2-1,3}=\dfrac{5,5}{0,9}=\dfrac{55}{9}\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{1,1.55}{9}=\dfrac{121}{18}\\y=\dfrac{1,3.55}{9}=\dfrac{143}{18}\\z=\dfrac{1,4.55}{9}=\dfrac{77}{9}\end{matrix}\right.\) Nghi ngờ bạn chép đề câu này sai, số xấu quá

Có: \(\dfrac{x-1}{2}=\dfrac{y+3}{4}=\dfrac{z-5}{6}\)
<=> \(\dfrac{3\left(x-1\right)}{3.2}=\dfrac{4\left(y+3\right)}{4.4}=\dfrac{5\left(z-5\right)}{6.5}\)
<=> \(\dfrac{3x-3}{6}=\dfrac{4y+12}{16}=\dfrac{5z-25}{30}\)
mà 5z-3x-4y=50
ADTCDTSBN ta có:\(\dfrac{3x-3}{6}=\dfrac{4y+12}{16}=\dfrac{5z-25}{30}=\dfrac{5z-25-\left(4y+12\right)-\left(3x-3\right)}{30-16-6}=\dfrac{5z-25-4y-12-3x+3}{8}=\dfrac{\left(5z-4y-3x\right)-\left(25+12-3\right)}{8}=\dfrac{50-34}{8}=2\)
Do đó: \(\dfrac{3x-3}{6}=2\) <=> \(\dfrac{x-1}{2}=2\) <=> x-1=4 <=> x=5
\(\dfrac{4y+12}{16}=2\) <=> \(\dfrac{y+3}{4}=2\) <=> y+3=8<=> y=5
\(\dfrac{5z-25}{30}=2\) <=> \(\dfrac{z-5}{6}=2\) <=> z-5=12 <=> z=17
Vậy x=5 , y=5 , z=17

\(\dfrac{x-1}{2}=\dfrac{y+3}{4}=\dfrac{z-5}{6}\Rightarrow\dfrac{5\left(z-5\right)}{30}=\dfrac{3\left(x-1\right)}{6}=\dfrac{4\left(y+3\right)}{16}=\dfrac{5\left(z-5\right)-3\left(x-1\right)-4\left(y+3\right)}{30-6-16}=\dfrac{5z-25-3x+3-4y-12}{8}=\dfrac{\left(5z-3x-4y\right)+\left(-25+3-12\right)}{8}=\dfrac{50+\left(-34\right)}{8}=\dfrac{16}{8}=2\)\(\Rightarrow\dfrac{x-1}{2}=2\Rightarrow x=5\\ \dfrac{y+3}{4}=4\Rightarrow y=13\\ \dfrac{z-5}{6}=2\Rightarrow z=17\)
Theo bài ra ta có :
\(\dfrac{x-1}{2}=\dfrac{y+3}{4}=\dfrac{z-5}{6}\\ \Rightarrow\dfrac{3\left(x-1\right)}{6}=\dfrac{4\left(y+3\right)}{16}=\dfrac{5\left(z-5\right)}{30}\\ \Rightarrow\dfrac{3x-3}{6}=\dfrac{4y+12}{16}=\dfrac{5z-25}{30}\\ \Rightarrow\dfrac{5z-25}{30}=\dfrac{3x-3}{6}=\dfrac{4y+12}{16}\)
\(5z-3x-4y=50\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được :
\(\dfrac{5z-25}{30}=\dfrac{3x-3}{6}=\dfrac{4y+12}{16}\\ =\dfrac{\left(5z-25\right)-\left(3x-3\right)-\left(4y+12\right)}{30-6-16}\\ =\dfrac{5z-25-3x+3-4y-12}{8}\\ =\dfrac{\left(5z-3x-4y\right)-\left(25-3+12\right)}{8}\\ =\dfrac{50-34}{8}\\ =\dfrac{16}{8}\\ =2\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{3x-3}{6}=2\Rightarrow3x-3=12\Rightarrow3x=15\Rightarrow x=5\\\dfrac{4y+12}{16}=2\Rightarrow4y+12=32\Rightarrow4y=20\Rightarrow y=5\\\dfrac{5z-25}{30}=2\Rightarrow5z-25=60\Rightarrow5z=85\Rightarrow z=17\end{matrix}\right.\)
\(\text{Vậy }x=5\\ y=5\\ z=17\)

a,3x=2y;7y=5z
=>\(\dfrac{x}{2}=\dfrac{y}{3};\dfrac{y}{5}=\dfrac{z}{7}\Rightarrow\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta co:
\(\dfrac{x}{10}=\dfrac{y}{15}=\dfrac{z}{21}=\dfrac{x-y+z}{10-15+21}=\dfrac{32}{16}=2\\ \Rightarrow x=2.10=20\\ y=2.15=30\\ z=2.21=42\)
Các câu sau tương tự
b,\(\dfrac{x}{3}\)=\(\dfrac{y}{4}\),\(\dfrac{y}{3}\)=\(\dfrac{z}{5}\) và 2x-3y+z=6
Từ đề bài ta có:
\(\dfrac{x}{3}\)=\(\dfrac{y}{4}\)\(\Rightarrow\)\(\dfrac{x}{9}\)=\(\dfrac{y}{12}\)(1)
\(\dfrac{y}{3}\)=\(\dfrac{z}{5}\)\(\Rightarrow\)\(\dfrac{y}{12}\)=\(\dfrac{z}{20}\)(2)
từ (1) và (2)\(\Rightarrow\)\(\dfrac{x}{9}\)=\(\dfrac{y}{12}\)=\(\dfrac{z}{20}\)\(\Rightarrow\)\(\dfrac{2x}{18}\)=\(\dfrac{3y}{36}\)=\(\dfrac{z}{20}\)
Áp dụng t/c dãy tỉ số bằng nhau,ta có:
\(\dfrac{2x}{18}\)=\(\dfrac{3y}{36}\)=\(\dfrac{z}{20}\)=\(\dfrac{2x-3y+z}{18-36+20}\)=\(\dfrac{6}{2}\)=3
\(\Rightarrow\)x=3.9=27
y=3.12=36
z=3.20=60
Vậy.....
chúc bạn học tốt,nhớ tick cho mình nha![]()

a/ Do \(x+y=22\Rightarrow y=22-x\)
\(\Rightarrow\dfrac{4+x}{7+22-x}=\dfrac{4}{7}\Leftrightarrow\dfrac{4+x}{29-x}=\dfrac{4}{7}\)
\(\Leftrightarrow7\left(4+x\right)=4\left(29-x\right)\Leftrightarrow28+7x=116-4x\)
\(\Leftrightarrow11x=88\Rightarrow x=8\)
\(\Rightarrow y=22-x=14\)
b/ \(\dfrac{x}{3}=\dfrac{y}{4}\Rightarrow y=\dfrac{4x}{3}\)
\(\dfrac{y}{5}=\dfrac{z}{6}\Rightarrow z=\dfrac{6y}{5}\) \(\Rightarrow z=\dfrac{6}{5}\left(\dfrac{4x}{3}\right)=\dfrac{8x}{5}\)
Vậy \(M=\dfrac{2x+3y+4z}{3x+4y+5z}=\dfrac{2x+3.\dfrac{4x}{3}+4.\dfrac{8x}{5}}{3x+4.\dfrac{4x}{3}+5.\dfrac{8x}{5}}\)
\(\Rightarrow M=\dfrac{x\left(2+4+\dfrac{32}{5}\right)}{x\left(3+\dfrac{16}{3}+8\right)}=\dfrac{\dfrac{62}{5}}{\dfrac{49}{3}}=\dfrac{186}{245}\)
Câu a:
Ta có: \(x+y=22\Rightarrow y=22-x\)
\(\Rightarrow\dfrac{4+x}{7+22-x}=\dfrac{4}{7}\Leftrightarrow\dfrac{4+x}{29-x}=\dfrac{4}{7}\)
\(\Leftrightarrow7\left(4+x\right)=4\left(29-x\right)\Leftrightarrow28+7x=116-4x\)
\(\Leftrightarrow11x=88\Rightarrow x=8\)
\(\Rightarrow y=22-x=22-8=14\)
Vậy \(x=8,y=14\)

a)vì\(\dfrac{x}{3}\)=\(\dfrac{y}{4}\)=\(\dfrac{z}{5}\)=>\(\dfrac{2x}{6}\)=\(\dfrac{3y}{12}\)=\(\dfrac{5z}{25}\)và 2x+3y+5z=86
áp dụng tính chất của dãy tỉ số bằng nhau ta có
\(\dfrac{2x}{6}\)=\(\dfrac{3y}{12}\)=\(\dfrac{5z}{25}\)=\(\dfrac{2x+3y+5z}{6+12+25}\)\(\dfrac{86}{43}\)=2
vì\(\dfrac{2x}{6}\)=2=>2x=2.6=12=>x=12:2=6
\(\dfrac{3y}{12}\)=2=>3y=12.2=24=>y=24:3=8
\(\dfrac{5z}{25}\)=2=>5z=25.2=50=>z=50:5=10
vậy x=6,y=8,z=10
vì\(\dfrac{x}{3}\)=\(\dfrac{y}{4}\)=>\(\dfrac{x}{9}\)=\(\dfrac{y}{12}\)(1)
\(\dfrac{y}{6}\)=\(\dfrac{z}{8}\)=>\(\dfrac{y}{12}\)=\(\dfrac{z}{16}\)(2)
từ (1)(2)=>\(\dfrac{x}{9}\)=\(\dfrac{y}{12}\)=\(\dfrac{z}{16}\)=>\(\dfrac{3x}{27}\)=\(\dfrac{2y}{24}\)=\(\dfrac{z}{16}\)và 3x-2y-z=13
áp dụng tính chất của dãy tỉ số bằng nhau ta có
\(\dfrac{3x}{27}\)=\(\dfrac{2y}{24}\)=\(\dfrac{z}{16}\)=\(\dfrac{3x-2y-z}{27-24-16}\)=\(\dfrac{13}{-13}\)=-1
vì\(\dfrac{3x}{27}\)=-1=>3x=-1.27=-27=>x=-27x;3=-9
\(\dfrac{2y}{24}\)=-1=>2y=-1.24=-24=>y=-24:2=-12
\(\dfrac{z}{16}\)=-1=>z=-1.16=-16
vậy...

\(\dfrac{x-2}{4}=\dfrac{y+1}{5}=\dfrac{z+3}{7}\)
\(\Rightarrow\dfrac{2\left(x-2\right)}{8}=\dfrac{y+1}{5}=\dfrac{2\left(z+3\right)}{14}\)
\(\Rightarrow\dfrac{2x-4}{8}=\dfrac{y+1}{5}=\dfrac{2z+6}{14}\)
Dựa vào tính chất dãy tỉ số bằng nhau ta có:
\(=\dfrac{2x-4+y+1-2z-6}{8+5-14}\)
\(=\dfrac{2x+y-2z-9}{-1}\)
\(=\dfrac{7-9}{-1}=2\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x-2}{4}=2\Rightarrow x-2=8\Rightarrow x=10\\\dfrac{y+1}{5}=2\Rightarrow y+1=10\Rightarrow y=9\\\dfrac{z+3}{7}=2\Rightarrow z+3=14\Rightarrow z=11\end{matrix}\right.\)