K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DT
Dang Tung
CTVHS
22 tháng 6 2023
Vì : \(\left(2x-5\right)^{2022}\ge0\forall x,\left(3y+4\right)^{2024}\ge0\forall y\\ =>\left(2x-5\right)^{2022}+\left(3y+4\right)^{2024}\ge0\)
Do đó đề bài xảy ra khi và chỉ khi :
\(\left\{{}\begin{matrix}\left(2x-5\right)^{2022}=0\\\left(3y+4\right)^{2024}=0\end{matrix}\right.\\ =>\left(x;y\right)=\left(\dfrac{5}{2};-\dfrac{4}{3}\right)\)
NT
22 tháng 6 2023
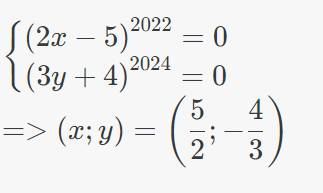Mình ko biết cách để làm ra đc kết quả này, có thể giải thích cụ thể hơn ko ạ?
DX
5
AH
Akai Haruma
Giáo viên
12 tháng 7 2021
Lời giải:
1.
$|4-x|\geq 0$ với mọi $x$
$|2y+1|\geq 0$ với mọi $y$
Do đó để $|4-x|+|2y+1|=0$ thì $|4-x|=|2y+1|=0$
$\Leftrightarrow x=4; y=\frac{-1}{2}$
2.
$|x-3|=|5-2x|$
$\Leftrightarrow x-3=5-2x$ hoặc $x-3=2x-5$
$\Leftrightarrow x=\frac{8}{3}$ hoặc $x=2$
12 tháng 7 2021
1 ) | 4 - x | + | 2y +1 | = 0
| Trường hợp 1 | Trường hợp 2 |
| x+1=0 | 2y-4=0 |
| x=0-1 | 2y=0+4 |
| x=-1 | 2y=2=>y=2 |
D
31 tháng 12 2017
a)
Ta có : vì|1/2-1/3+x| lớn hơn hoặc bằng 0
Còn -1/4-|y| bé hơn hoặc bằng 0
=> ko tồn tại x
b)
Ta có: |x-y| lớn hơn hoặc bằng 0 và|y+9/25| lớn hơn hoặc bằng 0 mà:
| x-y|+ |y+9/25| =0 => |x-y| =0 và |y+9/25|=0
Xét |y+9/25| có:
| y+9/25|=0 => y+9/25=0 => y=-9/25
Thay y = -9/25 vào |x-y| =0 => x=-9/25
Vậy x=y=-9/25
MV
0
WJ
0
DM
0