Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=\left(2x+1\right)\left(x^2+1\right)+\dfrac{4}{2x+1}\) (chia đa thức)
Để A nguyên \(\Rightarrow4⋮2x+1\Rightarrow\left(2x+1\right)=\left\{-4;-2;-1;1;2;4\right\}\)
\(\Rightarrow x=\left\{-\dfrac{5}{2};-\dfrac{3}{2};-1;0;\dfrac{1}{2};\dfrac{3}{2}\right\}\)
x thỏa mãn đk đề bài là \(x=\left\{-1;0\right\}\)

1) a) Căn thức có nghĩa \(\Leftrightarrow4-2x\ge0\Leftrightarrow2x\le4\Leftrightarrow x\le2\)
b) Thay x = 2 vào biểu thức A, ta được: \(A=\sqrt{4-2.2}=\sqrt{0}=0\)
Thay x = 0 vào biểu thức A, ta được: \(A=\sqrt{4-2.0}=\sqrt{4}=2\)
Thay x = 1 vào biểu thức A, ta được: \(A=\sqrt{4-2.1}=\sqrt{2}\)
Thay x = -6 vào biểu thức A, ta được: \(A=\sqrt{4-2.\left(-6\right)}=\sqrt{16}=4\)
Thay x = -10 vào biểu thức A, ta được: \(A=\sqrt{4-2.\left(-10\right)}=\sqrt{24}=2\sqrt{6}\)
c) \(A=0\Leftrightarrow\sqrt{4-2x}=0\Leftrightarrow4-2x=0\Leftrightarrow x=2\)
\(A=5\Leftrightarrow\sqrt{4-2x}=5\Leftrightarrow4-2x=25\Leftrightarrow x=\frac{-21}{2}\)
\(A=10\Leftrightarrow\sqrt{4-2x}=10\Leftrightarrow4-2x=100\Leftrightarrow x=-48\)

=>y=1-2x và mx+2(1-2x)=3
=>y=1-2x và mx+2-4x=3
=>y=1-2x và x(m-4)=1
=>x=1/m-4 và y=1-2/m-4=m-4-2/m-4=m-6/m-4
P=3x+y
=3/m-4+m-6/m-4
=m-3/m-4
Để P nguyên thì m-4+1 chia hết cho m-4
=>\(m-4\in\left\{1;-1\right\}\)
=>\(m\in\left\{5;3\right\}\)

\(A=\frac{x}{x^2+1}+\frac{5\left(x^2+1\right)}{2x}=\frac{x}{x^2+1}+\frac{x^2+1}{4x}+\frac{9}{4}.\frac{x^2+1}{x}\)
\(\ge2\sqrt{\frac{x}{x^2+1}.\frac{x^2+1}{4x}}+\frac{9}{4}.\frac{2\sqrt{x^2.1}}{x}=1+\frac{9}{2}=\frac{11}{2}\)
Dấu "=" xảy ra khi \(\left(\frac{x}{x^2+1}=\frac{x^2+1}{4x}\text{ và }x^2=1\right)\Leftrightarrow x=1\)
Vậy GTNN của biểu thức là 11/2.

\(P\le\sqrt{2\left(3x-5+7-3x\right)}=2\)
\(P_{max}=2\) khi \(3x-5=7-3x\Rightarrow x=2\)
\(A=2\left(x-1\right)+\dfrac{9}{x-1}+2\ge2\sqrt{\dfrac{18\left(x-1\right)}{x-1}}+2=6\sqrt{2}+2\)
\(A_{min}=6\sqrt{2}+2\) khi \(x=\dfrac{2+3\sqrt{2}}{2}\)

1:
\(A=\dfrac{9}{x-\sqrt{x}-2}+\dfrac{2\sqrt{x}+5}{\sqrt{x}+1}-\dfrac{\sqrt{x}-1}{\sqrt{x}-2}\)
\(=\dfrac{9}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}+\dfrac{2\sqrt{x}+5}{\sqrt{x}+1}-\dfrac{\sqrt{x}-1}{\sqrt{x}-2}\)
\(=\dfrac{9+\left(2\sqrt{x}+5\right)\left(\sqrt{x}-2\right)-\left(\sqrt{x}-1\right)\cdot\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{9+2x-4\sqrt{x}+5\sqrt{x}-10-x+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{x+\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
Để A là số nguyên thì \(\sqrt{x}⋮\sqrt{x}-2\)
=>\(\sqrt{x}-2+2⋮\sqrt{x}-2\)
=>\(\sqrt{x}-2\in\left\{1;-1;2;-2\right\}\)
=>\(\sqrt{x}\in\left\{3;1;4;0\right\}\)
=>\(x\in\left\{9;1;16;0\right\}\)
2:
\(\text{Δ}=\left(-2m-3\right)^2-4m\)
\(=4m^2+12m+9-4m\)
\(=4m^2+5m+9\)
\(=\left(2m\right)^2+2\cdot2m\cdot\dfrac{5}{4}+\dfrac{25}{16}+\dfrac{56}{16}\)
\(=\left(2m+\dfrac{5}{4}\right)^2+\dfrac{56}{16}>=\dfrac{56}{16}>0\)
=>Phương trình luôn có hai nghiệm phân biệt
\(x_1^2+x_2^2=9\)
=>\(\left(x_1+x_2\right)^2-2x_1x_2=9\)
=>\(\left(2m+3\right)^2-2m=9\)
=>\(4m^2+12m+9-2m-9=0\)
=>4m^2+10m=0
=>2m(2m+5)=0
=>m=0 hoặc m=-5/2

\(P=\left(x^2+y^2\right)^2-2x^2y^2-4xy+3=\left[\left(x+y\right)^2-2xy\right]^2-2x^2y^2-4xy+3\)
\(=\left(16-2xy\right)^2-2x^2y^2-4xy+3=2x^2y^2-68xy+259\)
\(4=x+y\ge2\sqrt[]{xy}\Rightarrow0\le xy\le4\)
Đặt \(xy=a\Rightarrow0\le a\le4\)
\(P=2a^2-68a+259=259-2a\left(34-a\right)\le259\)
\(P_{max}=259\) khi \(a=0\) hay \(\left(x;y\right)=\left(4;0\right);\left(0;4\right)\)
\(P=\left(2a^2-68a+240\right)+19=2\left(4-a\right)\left(30-a\right)+19\ge19\)
\(P_{min}=19\) khi \(a=4\) hay \(x=y=2\)
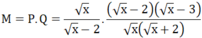
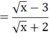
a) Giá trị của biểu thức 2x + 1 là số dương, ta có bất đẳng thức:
2x + 1 > 0
2x > - 1
x > \( - \frac{1}{2}\)
Vậy x > \( - \frac{1}{2}\) thì giá trị của biểu thức 2x + 1 là số dương.
b) Giá trị biểu thức 3x – 5 là số âm, ta có bất đẳng thức:
3x – 5 < 0
3x < 5
x < \(\frac{5}{3}\)
Vậy x < \(\frac{5}{3}\) thì giá trị biểu thức 3x – 5 là số âm.